题目内容
函数f(x)是R上以2为周期的奇函数,已知当x∈(0,1)时,f(x)=log2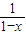 ,则f(x)在区间(1,2)上是( )
,则f(x)在区间(1,2)上是( )A.减函数,且f(x)<0
B.增函数,且f(x)<0
C.减函数,且f(x)>0
D.增函数,且f(x)>0
【答案】分析:欲求f(x)在区间(1,2)上的性质,可先求出其解析式,根据解析式研究性质.
解答:解:设-1<x<0,则0<-x<1,∴f(-x)=log2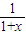 ,
,
又f(x)=-f(x),∴f(x)=log2(1+x),
∴1<x<2时,-1<x<-2<0,
∴f(x)=f(x-2)=log2(x-1).
∴f(x)在区间(1,2)上是增函数,且f(x)<0.
故选B.
点评:已知奇函数的一侧的解析式,可以求出其关于原点对称的另一侧的解析式,这是奇函数的一个重要应用.
解答:解:设-1<x<0,则0<-x<1,∴f(-x)=log2
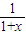 ,
,又f(x)=-f(x),∴f(x)=log2(1+x),
∴1<x<2时,-1<x<-2<0,
∴f(x)=f(x-2)=log2(x-1).
∴f(x)在区间(1,2)上是增函数,且f(x)<0.
故选B.
点评:已知奇函数的一侧的解析式,可以求出其关于原点对称的另一侧的解析式,这是奇函数的一个重要应用.

练习册系列答案
相关题目
函数f(x)是R上以2为周期的奇函数,已知当x∈(0,1)时,f(x)=log2
,则f(x)在区间(1,2)上是( )
| 1 |
| 1-x |
| A、减函数,且f(x)<0 |
| B、增函数,且f(x)<0 |
| C、减函数,且f(x)>0 |
| D、增函数,且f(x)>0 |
设函数f(x)是R上以5为周期的可导偶函数,则曲线y=f(x)在x=5处的切线的斜率为( )
A、-
| ||
| B、0 | ||
C、
| ||
| D、5 |
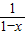 ,则f(x)在区间(1,2)上是( )
,则f(x)在区间(1,2)上是( )