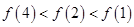题目内容
函数 对任意a,b
对任意a,b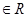 都有
都有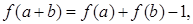 当
当 时,
时,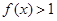 .
.
(1)求证: 在R上是增函数. (2)若
在R上是增函数. (2)若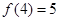 ,解不等式
,解不等式 .
.
【答案】
(1)见解析(2) 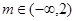
【解析】
试题分析:(1)隐函数的问题,关键是对所给的字母进行适当的赋值发现一些隐藏的性质.本题的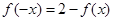 要挖掘出来.因为解析式不知道,所以要根据增函数的定义证明.(2)由(1)函数递增,再求函数值3所对的自变量,得出两个自变量间的关系.从而得解.
要挖掘出来.因为解析式不知道,所以要根据增函数的定义证明.(2)由(1)函数递增,再求函数值3所对的自变量,得出两个自变量间的关系.从而得解.
试题解析: (1)证明: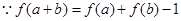 ,令
,令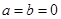 ,
,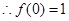 ,再令
,再令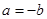 ,
,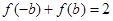 ,即
,即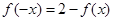 .对任意
.对任意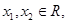 设
设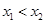 ,
,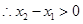 ,
, ,又由
,又由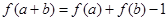 可得,
可得,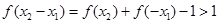 ,
,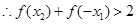 ,
,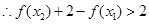 ,即
,即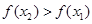 .又因为
.又因为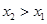 ,所以
,所以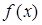 在R上是增函数.
在R上是增函数.
(2)由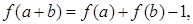
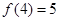 令
令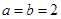 ,
,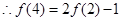 ,
,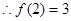 ,所以f(3m-4)<3可化为f(3m-4)<f(2),又因为f(x)在R上递增,所以3m-4<2,解得:m<2,即
,所以f(3m-4)<3可化为f(3m-4)<f(2),又因为f(x)在R上递增,所以3m-4<2,解得:m<2,即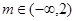 .
.
考点:1.隐函数的问题.2.函数的单调性.3.利用函数的单调性解不等式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 对任意的实数
对任意的实数 都有
都有 ,且
,且 ,则
,则
 B.
B. C.
C. D.
D.
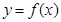 对任意的实数
对任意的实数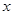 都有
都有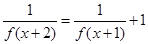 ,且
,且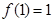 ,则
,则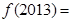 ( )
( )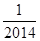 B.
B.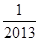 C.
C. D.
D.
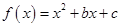 对任意的实数
对任意的实数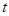 都有
都有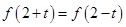 ,则( )
,则( )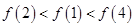 (B)
(B) 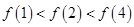
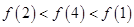 (D)
(D)