题目内容
(本题12分)
火车站有某公司等待运送的甲种货物1530吨,乙种货物1150吨。现计划用A、B两种型号的车厢共50节运送这批货物。已知35吨甲种货物和15吨乙种货物可装满一节A型车厢;25吨甲种货物和35吨乙种货物可装满一节B型车厢。
(Ⅰ)请你根据以上条件,安排A、B两种型号的车厢的节数,列出所有可能的方案;
(Ⅱ)若每节A型车厢的运费是0.5万元,每节B型车厢的运费是0.8万元,哪种方案的运费最少?请你说明理由.
火车站有某公司等待运送的甲种货物1530吨,乙种货物1150吨。现计划用A、B两种型号的车厢共50节运送这批货物。已知35吨甲种货物和15吨乙种货物可装满一节A型车厢;25吨甲种货物和35吨乙种货物可装满一节B型车厢。
(Ⅰ)请你根据以上条件,安排A、B两种型号的车厢的节数,列出所有可能的方案;
(Ⅱ)若每节A型车厢的运费是0.5万元,每节B型车厢的运费是0.8万元,哪种方案的运费最少?请你说明理由.
略
解:(Ⅰ)设安排A型车厢x节,B型车厢y节,总运费为z万元.则由题意可得
 约束条件为
约束条件为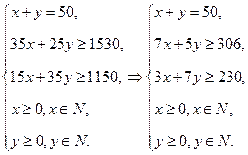
 目标函数为
目标函数为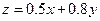 .
.
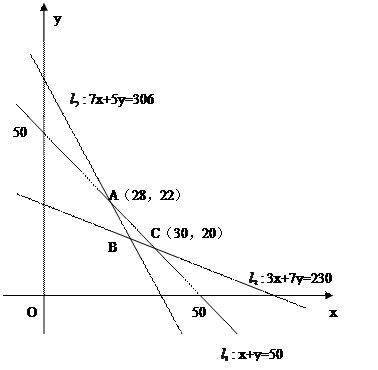
作出二元一次不等式组所表示的可行域,
如图所示。设直线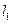 :x+y=50、
:x+y=50、
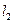 :7x+5y=306、
:7x+5y=306、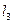 :3x+7y=230.
:3x+7y=230.
解方程组可得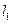 与
与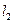 的交点A的坐标;
的交点A的坐标;
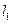 与
与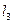 的交点C的坐标。
的交点C的坐标。
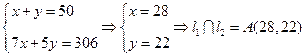
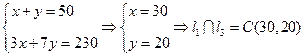
根据图象可知:28≤x≤30, 20≤y≤22,x,y∈N,且x+y=50.
于是安排A、B两种型号的车厢的节数的所有可能方案为:
方案1:安排A型车厢28节,B型车厢22节;
方案2:安排A型车厢29节,B型车厢21节;
方案3:安排A型车厢30节,B型车厢20节。
(Ⅱ)考虑目标函数为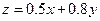 ,将它变形为
,将它变形为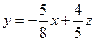 ,由图可见,当直线
,由图可见,当直线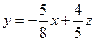 经过可行域(线段AC)上的点C时,截距
经过可行域(线段AC)上的点C时,截距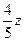 最小,即z最小
最小,即z最小 。z=0.5×30+0.8×20=31(万元) 即方案3:安排A型车厢30节,B型车厢20节,最少的运费为31万元。
。z=0.5×30+0.8×20=31(万元) 即方案3:安排A型车厢30节,B型车厢20节,最少的运费为31万元。
 约束条件为
约束条件为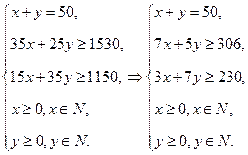
 目标函数为
目标函数为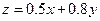 .
.作出二元一次不等式组所表示的可行域,
如图所示。设直线
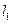 :x+y=50、
:x+y=50、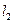 :7x+5y=306、
:7x+5y=306、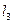 :3x+7y=230.
:3x+7y=230.解方程组可得
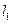 与
与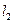 的交点A的坐标;
的交点A的坐标; 与
与 的交点C的坐标。
的交点C的坐标。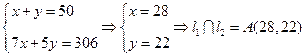
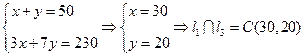
根据图象可知:28≤x≤30, 20≤y≤22,x,y∈N,且x+y=50.
于是安排A、B两种型号的车厢的节数的所有可能方案为:
方案1:安排A型车厢28节,B型车厢22节;
方案2:安排A型车厢29节,B型车厢21节;
方案3:安排A型车厢30节,B型车厢20节。
(Ⅱ)考虑目标函数为
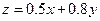 ,将它变形为
,将它变形为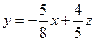 ,由图可见,当直线
,由图可见,当直线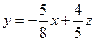 经过可行域(线段AC)上的点C时,截距
经过可行域(线段AC)上的点C时,截距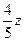 最小,即z最小
最小,即z最小 。z=0.5×30+0.8×20=31(万元) 即方案3:安排A型车厢30节,B型车厢20节,最少的运费为31万元。
。z=0.5×30+0.8×20=31(万元) 即方案3:安排A型车厢30节,B型车厢20节,最少的运费为31万元。
练习册系列答案
相关题目
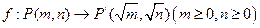 .设点
.设点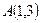 ,
,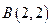 ,点M 是线段AB上一动点,
,点M 是线段AB上一动点,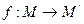 .当点M在线段AB上从点A开始运动到点B结束时,点M的对应点
.当点M在线段AB上从点A开始运动到点B结束时,点M的对应点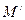 所经过的路线长度为 ( )
所经过的路线长度为 ( )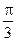
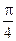
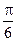
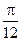
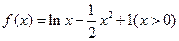 ,则函数
,则函数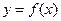
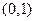 ,
,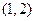 内均有零点
内均有零点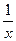 +
+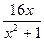 的最小值为 ( )
的最小值为 ( )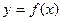 在区间(a,b)(
在区间(a,b)(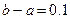 )上有唯一零点,如果用“二分法”求这个零点(精确到0.000 1)的近似值,那么将区间(a,b)等分的次数至多是 。
)上有唯一零点,如果用“二分法”求这个零点(精确到0.000 1)的近似值,那么将区间(a,b)等分的次数至多是 。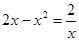 的正根个数为_______个.
的正根个数为_______个. 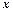 )的定义域为R,若存在与
)的定义域为R,若存在与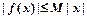 对一切实数
对一切实数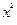 ②f(
②f(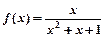
 ④
④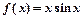 其中是“有界泛函”的个数为( )
其中是“有界泛函”的个数为( )