题目内容
（理）已知双曲线
-
=1的左焦点为F1，左、右顶点为A1、A2，P为双曲线上任意一点，则分别以线段PF1，A1A2为直径的两个圆的位置关系为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、相交 | B、相切 |
| C、相离 | D、以上情况都有可能 |
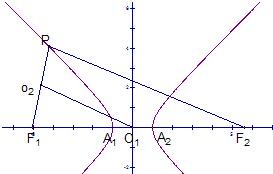
分析：画出图象，考查两圆的位置关系，就是看圆心距与半径和或与半径差的关系，分情况P在左支、右支，推导结论．
解答：解：如图所示，若P在双曲线坐支，则|O1O2|=
|PF2|=
(|PF1|+2a)=
|PF1|+a=r1+r2，
即圆心距为半径之和，两圆外切；
若P在双曲线右支，则|O1O2|=r1-r2，两圆内切，
所以两圆相切；
故选B．
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即圆心距为半径之和，两圆外切；若P在双曲线右支，则|O1O2|=r1-r2，两圆内切，
所以两圆相切；
故选B．
点评：本题考查圆与圆的位置关系及其判定，双曲线的应用，考查数形结合思想方法，是基础题．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
-x2=1,则其渐近线方程是__________,离心率e=__________.