题目内容
已知数列{an}的前n项和为Sn,且对一切正整数n都有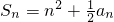 .
.
(I)求证:an+1+an=4n+2;
(II)求数列{an}的通项公式;
(III)是否存在实数a,使不等式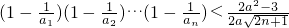 对一切正整数n都成立?若存在,求出a的取值范围;若不存在,请说明理由.
对一切正整数n都成立?若存在,求出a的取值范围;若不存在,请说明理由.
解:(I)∵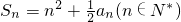 ,
,
∴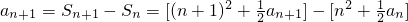
=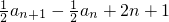 ,
,
∴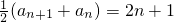 ,
,
即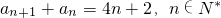 .
.
(II)在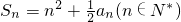 中,
中,
令n=1,得a1=2,代入(I)得a2=4.
∵an+1+an=4n+2,∴an+2+an+1=4n+6,
两式相减,得:an+2-an=4,
∴数列{an}的偶数项a2,a4,a6,…,a26,…依次构成一个等差数列,
且公差为d=4,
∴当n为偶数时,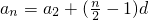 =
=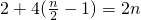 ,
,
当n为奇数时,n+1为偶数,由上式及(I)知:
an=4n+2-an+1=4n+2-2(n+1)=2n,
∴数列{an}的通项公式是an=2n.
(III)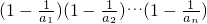 <
<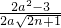 ,
,
等价于 ,
,
令f(n)= ,
,
则由(II)知f(n)>0,
∴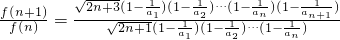
═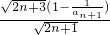
=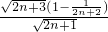
=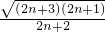
=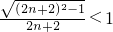 .
.
∴f(n+1)<f(n),即f(n)的值随n的增大而减小,
∴n∈N*时,f(n)的最大值为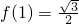 ,若存在实数a,符合题意,
,若存在实数a,符合题意,
则必有: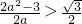 ,
,
即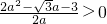 ,
,
它等价于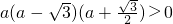 ,
,
解得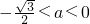 ,或
,或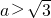 ,
,
因此,存在实数a,符合题意,
其取值范围为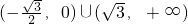 .
.
分析:(I)由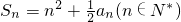 ,知
,知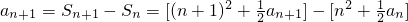 ,由此能够导出
,由此能够导出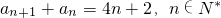 .
.
(II)在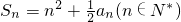 中,令n=1,得a1=2,代入(I)得a2=4.由an+1+an=4n+2,知an+2+an+1=4n+6,故an+2-an=4,由此能导出数列{an}的通项公式是an=2n.
中,令n=1,得a1=2,代入(I)得a2=4.由an+1+an=4n+2,知an+2+an+1=4n+6,故an+2-an=4,由此能导出数列{an}的通项公式是an=2n.
(III)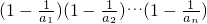 <
<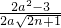 等价于
等价于 ,令f(n)=
,令f(n)= ,则f(n)>0,由此能够导出存在实数a,符合题意,并能求出其取值范围.
,则f(n)>0,由此能够导出存在实数a,符合题意,并能求出其取值范围.
点评:本题考查数列和不等式的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.
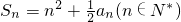 ,
,∴
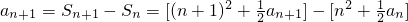
=
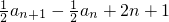 ,
,∴
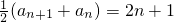 ,
,即
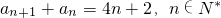 .
.(II)在
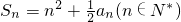 中,
中,令n=1,得a1=2,代入(I)得a2=4.
∵an+1+an=4n+2,∴an+2+an+1=4n+6,
两式相减,得:an+2-an=4,
∴数列{an}的偶数项a2,a4,a6,…,a26,…依次构成一个等差数列,
且公差为d=4,
∴当n为偶数时,
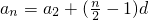 =
=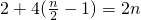 ,
,当n为奇数时,n+1为偶数,由上式及(I)知:
an=4n+2-an+1=4n+2-2(n+1)=2n,
∴数列{an}的通项公式是an=2n.
(III)
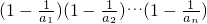 <
<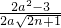 ,
,等价于
 ,
,令f(n)=
 ,
,则由(II)知f(n)>0,
∴
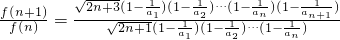
═
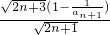
=
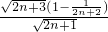
=
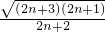
=
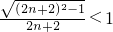 .
.∴f(n+1)<f(n),即f(n)的值随n的增大而减小,
∴n∈N*时,f(n)的最大值为
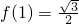 ,若存在实数a,符合题意,
,若存在实数a,符合题意,则必有:
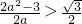 ,
,即
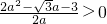 ,
,它等价于
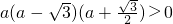 ,
,解得
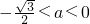 ,或
,或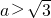 ,
,因此,存在实数a,符合题意,
其取值范围为
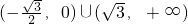 .
.分析:(I)由
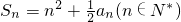 ,知
,知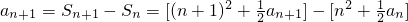 ,由此能够导出
,由此能够导出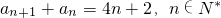 .
.(II)在
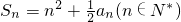 中,令n=1,得a1=2,代入(I)得a2=4.由an+1+an=4n+2,知an+2+an+1=4n+6,故an+2-an=4,由此能导出数列{an}的通项公式是an=2n.
中,令n=1,得a1=2,代入(I)得a2=4.由an+1+an=4n+2,知an+2+an+1=4n+6,故an+2-an=4,由此能导出数列{an}的通项公式是an=2n.(III)
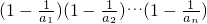 <
<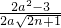 等价于
等价于 ,令f(n)=
,令f(n)= ,则f(n)>0,由此能够导出存在实数a,符合题意,并能求出其取值范围.
,则f(n)>0,由此能够导出存在实数a,符合题意,并能求出其取值范围.点评:本题考查数列和不等式的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |