题目内容
已知圆的方程为x2+y2-6x-8y=0，设该圆过点(3,5)的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积为（ ）
A．10 | B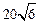． | C．  | D． |
B
可知点(3,5)在圆内,所以最长弦AC为圆的直径.设AC与BD的交点为M(3,5)
x2+y2-6x-8y=0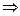
(x-3)2+(y-4)2="25" 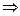AC=10,圆心O(3,4)
∵BD为最短弦
∴AC与BD相垂直,垂足为M,所以OM=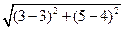
=1
∴BD=2BM=2
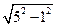=4
∵S四边形ABCD=S△ABD+S△BDC=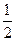
×BD×MA+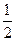×BD×MC=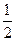×BD×(MA+MC) =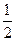×BD×AC
∴S四边形ABCD=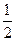×4×10=20.
x2+y2-6x-8y=0
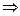(x-3)2+(y-4)2="25" 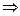AC=10,圆心O(3,4)∵BD为最短弦
∴AC与BD相垂直,垂足为M,所以OM=
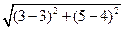=1∴BD=2BM=2
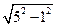=4∵S四边形ABCD=S△ABD+S△BDC=
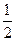×BD×MA+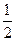×BD×MC=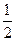×BD×(MA+MC) =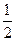×BD×AC∴S四边形ABCD=
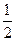×4×10=20.
练习册系列答案
相关题目
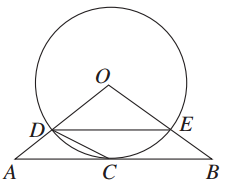
，求⊙O的半径r的长．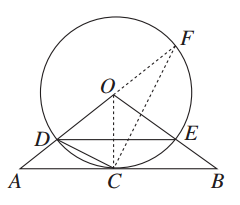
：
的离心率为
，以原点为圆心、椭圆的短半轴长为半径的圆与直线
相切．
的切线
与椭圆相交于A、B两点，求证：以AB为直径的圆过原点．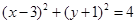
上的动点，Q是直线
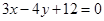上的动点，则
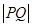的最小值为（ ）
和圆：
交于A、B两点，则AB的垂直平分线的方程是（ ）．
B．
C． 
D．
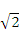，0）引直线ι与曲线
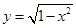交于A,B两点 ，O为坐标原点，当△AOB的面积取最大值时，直线ι的斜率等于（ ）
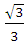B.-
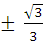D-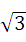
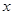轴上，半径长是
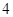，且与直线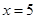
相切的圆的方程是 ．
：
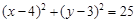，过圆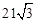
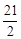
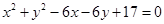所走过的最短路程为 ．