题目内容
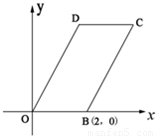
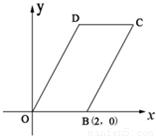
如图,已知四边形OBCD是平行四边形,|OB|=2,|OD|=4,∠DOB=60°,直线x=t(0<t<4)分别交平行四边行两边于不同的两点M、N.(1)求点C和D的坐标,分别写出OD、DC和BC所在直线方程;
(2)写出OMN的面积关于t的表达式s(t),并求当t为何值时s(t)有最大值,并求出这个最大值.
【答案】分析:(1)先求出得D、C的坐标,进而利用直线方程的四种形式即可求出;
(2)先写出△OMN的解析式,进而即可得出其最大值.
解答:解:(1)设点D(x,y),则x=|OD|cos60°= ,y=|OD|sin60°=
,y=|OD|sin60°= ,∴点D
,∴点D .
.
∴点C的横坐标=2+2=4,纵坐标= ,即C
,即C .
.
①∵ ,∴直线OD的方程为
,∴直线OD的方程为 ;
;
②∵BC∥OD,∴ ,根据点斜式得直线BC的方程为
,根据点斜式得直线BC的方程为 ,即
,即 ;
;
③∵DC∥x轴,且点D的纵坐标为 ,
,
∴直线DC的直线方程为 .
.
(2)由题意作出图形.
①当0<t≤2时,s(t)=S△OMN= =
= ,可知当t=2时,s(t)取得最大值为
,可知当t=2时,s(t)取得最大值为 ,
,
∴ ;
;
②当2<t<4时,联立 解得
解得 ,即N
,即N ,
,
又可知M ,∴|MN|=
,∴|MN|= =
= .
.
∴s(t)=S△OMN= =
= .
.
∵函数s(t)在(2,4)上单调递减,
∴s(t)<s(2)= .
.
综上可知:当t=2时,s(t0取得最大值 .
.
点评:熟练掌握直线方程的四种形式和正确得出△OMN的面积的表达式是解题的关键.
(2)先写出△OMN的解析式,进而即可得出其最大值.
解答:解:(1)设点D(x,y),则x=|OD|cos60°=
 ,y=|OD|sin60°=
,y=|OD|sin60°= ,∴点D
,∴点D .
.
∴点C的横坐标=2+2=4,纵坐标=
 ,即C
,即C .
.①∵
 ,∴直线OD的方程为
,∴直线OD的方程为 ;
;②∵BC∥OD,∴
 ,根据点斜式得直线BC的方程为
,根据点斜式得直线BC的方程为 ,即
,即 ;
;③∵DC∥x轴,且点D的纵坐标为
 ,
,∴直线DC的直线方程为
 .
.(2)由题意作出图形.
①当0<t≤2时,s(t)=S△OMN=
 =
= ,可知当t=2时,s(t)取得最大值为
,可知当t=2时,s(t)取得最大值为 ,
,∴
 ;
;②当2<t<4时,联立
 解得
解得 ,即N
,即N ,
,又可知M
 ,∴|MN|=
,∴|MN|= =
= .
.∴s(t)=S△OMN=
 =
= .
.∵函数s(t)在(2,4)上单调递减,
∴s(t)<s(2)=
 .
.综上可知:当t=2时,s(t0取得最大值
 .
.点评:熟练掌握直线方程的四种形式和正确得出△OMN的面积的表达式是解题的关键.

练习册系列答案
相关题目
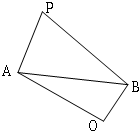 如图,已知四边形PAOB中,PA⊥OA,PB⊥OB.且PA=5,PB=8,AB=7
如图,已知四边形PAOB中,PA⊥OA,PB⊥OB.且PA=5,PB=8,AB=7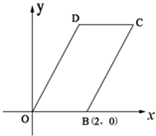 如图,已知四边形OBCD是平行四边形,|OB|=2,|OD|=4,∠DOB=60°,直线x=t(0<t<4)分别交平行四边行两边于不同的两点M、N.
如图,已知四边形OBCD是平行四边形,|OB|=2,|OD|=4,∠DOB=60°,直线x=t(0<t<4)分别交平行四边行两边于不同的两点M、N.