题目内容
已知x、y、z∈R+,且x+y+z=1,求xy2z+xyz2的最大值.解析:xy2z+xyz2=xyz(y+z)
=x(1-x)yz≤x(1-x)·(![]() )2
)2
=x(1-x)·![]()
=![]() ·3x·(1-x)·(1-x)·(1-x)
·3x·(1-x)·(1-x)·(1-x)
≤![]() ·(
·(![]() )4=
)4=![]() ,
,
当且仅当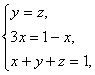 即
即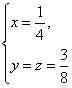 时,
时,
(xy2z+xyz2)max=![]() .
.

练习册系列答案
相关题目
题目内容
已知x、y、z∈R+,且x+y+z=1,求xy2z+xyz2的最大值.解析:xy2z+xyz2=xyz(y+z)
=x(1-x)yz≤x(1-x)·(![]() )2
)2
=x(1-x)·![]()
=![]() ·3x·(1-x)·(1-x)·(1-x)
·3x·(1-x)·(1-x)·(1-x)
≤![]() ·(
·(![]() )4=
)4=![]() ,
,
当且仅当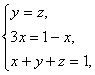 即
即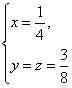 时,
时,
(xy2z+xyz2)max=![]() .
.
