题目内容
 你作为工厂的一名设计师,准备为工厂修建一个如图所示的长方体形无盖蓄水池,其容积为40立方米,深度为2米.池底每平方米的造价为15元,池壁每平方米的造价为10元.工厂审计部门要你根据工程设计申请经费,你如何设计这个水池才能使得申请经费最低?(经费单位:元,结果取整数,可能用到的数据:
你作为工厂的一名设计师,准备为工厂修建一个如图所示的长方体形无盖蓄水池,其容积为40立方米,深度为2米.池底每平方米的造价为15元,池壁每平方米的造价为10元.工厂审计部门要你根据工程设计申请经费,你如何设计这个水池才能使得申请经费最低?(经费单位:元,结果取整数,可能用到的数据:| 2 |
| 5 |
分析:确定底面积,侧壁面积,建立函数关系式,利用基本不等式,即可求得结论.
解答:解:由题意,底面积是20平方米,设池底长为xm,则宽为
m,∴侧壁面积:4x+
(x>0)平方米
∴总造价为
∵x>0,∴y≥300+160
≈652元,当且仅当4x=
,即x=2
≈4.4m时,申请经费最低
此时,池底为边长为4.4m的正方形.
| 20 |
| x |
| 80 |
| x |
∴总造价为
|
∵x>0,∴y≥300+160
| 5 |
| 80 |
| x |
| 5 |
此时,池底为边长为4.4m的正方形.
点评:本题考查利用数学知识解决实际问题,考查基本不等式的运用,确定函数解析式是关键.

练习册系列答案
相关题目
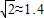 ,
,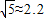 )
)
