题目内容
已知函数 ,b=f(2),c=f(3),则
,b=f(2),c=f(3),则
- A.c<a<b
- B.b<c<a
- C.c<b<a
- D.a<b<c
A
分析:由条件可得:函数y=f(x)的图象关于直线x= 对称,当
对称,当  时,f(x)=x+sinx,是增函数,故函数y=f(x)在(
时,f(x)=x+sinx,是增函数,故函数y=f(x)在(  ,π )上是减函数,结合图象特征,得到答案.
,π )上是减函数,结合图象特征,得到答案.
解答:∵函数y=f(x)满足f(x)=f(π-x),
∴函数y=f(x)的图象关于直线x= 对称,
对称,
因为当 时,f(x)=x+sinx,
时,f(x)=x+sinx,
所以f′(x)=1+cosx>0在 上恒成立,
上恒成立,
所以函数在 上是增函数,
上是增函数,
所以函数y=f(x)在( ,π )上是减函数.
,π )上是减函数.
因为2距离对称轴最近,其次是1,最远的时3,
所以根据函数的有关性质可得:f(3)<f(1)<f(2),即 c<a<b,
故选A.
点评:本题考查正弦函数的单调性,图象的对称性,判断函数y=f(x)的图象关于直线x= 对称,且当
对称,且当  时,f(x)=x+sinx 是增函数,是解题的关键.
时,f(x)=x+sinx 是增函数,是解题的关键.
分析:由条件可得:函数y=f(x)的图象关于直线x=
 对称,当
对称,当  时,f(x)=x+sinx,是增函数,故函数y=f(x)在(
时,f(x)=x+sinx,是增函数,故函数y=f(x)在(  ,π )上是减函数,结合图象特征,得到答案.
,π )上是减函数,结合图象特征,得到答案.解答:∵函数y=f(x)满足f(x)=f(π-x),
∴函数y=f(x)的图象关于直线x=
 对称,
对称,因为当
 时,f(x)=x+sinx,
时,f(x)=x+sinx,所以f′(x)=1+cosx>0在
 上恒成立,
上恒成立,所以函数在
 上是增函数,
上是增函数,所以函数y=f(x)在(
 ,π )上是减函数.
,π )上是减函数.因为2距离对称轴最近,其次是1,最远的时3,
所以根据函数的有关性质可得:f(3)<f(1)<f(2),即 c<a<b,
故选A.
点评:本题考查正弦函数的单调性,图象的对称性,判断函数y=f(x)的图象关于直线x=
 对称,且当
对称,且当  时,f(x)=x+sinx 是增函数,是解题的关键.
时,f(x)=x+sinx 是增函数,是解题的关键. 
练习册系列答案
相关题目
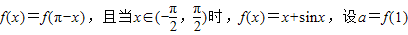 ,b=f(2),c=f(3),则( )
,b=f(2),c=f(3),则( )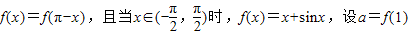 ,b=f(2),c=f(3),则( )
,b=f(2),c=f(3),则( )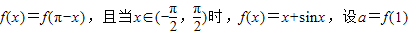 ,b=f(2),c=f(3),则( )
,b=f(2),c=f(3),则( )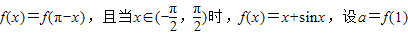 ,b=f(2),c=f(3),则( )
,b=f(2),c=f(3),则( )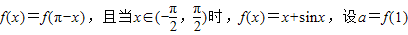 ,b=f(2),c=f(3),则( )
,b=f(2),c=f(3),则( )