题目内容
(2010·北京理,15)已知函数f(x)=2cos2x+sin2x-4cosx.
(1)求f(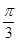 )的值;
)的值;
(2)求f(x)的最大值和最小值.
【答案】
(1)-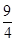 .(2)当cosx=-1时,f(x)取最大值6;当cosx=
.(2)当cosx=-1时,f(x)取最大值6;当cosx=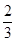 时,f(x)取最小值-
时,f(x)取最小值-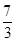 .
.
【解析】本题考查了三角函数的化简求值及二次函数在区间上的最值.(1)可直接求解,(2)化简后转化为关于cosx的二次函数,求值即可.
(1)f(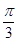 )=2cos
)=2cos +sin2
+sin2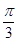 -4cos
-4cos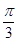 =-1+
=-1+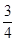 -2=-
-2=-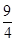 .
.
(2)f(x)=2(2cos2x-1)+(1-cos2x)-4cosx
=3cos2x-4cosx-1=3(cosx-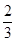 )2-
)2-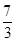 ,x∈R
,x∈R
因为cosx∈[-1,1],所以当cosx=-1时,f(x)取最大值6;当cosx=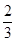 时,f(x)取最小值-
时,f(x)取最小值-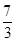 .
.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目