��Ŀ����
��֪����f��x��=lnx��g��x��=��m+1��x2��x��m�٩�1����
��I��������y=f��x����y=g��x����ͼ���ڹ�����P������ͬ�����ߣ���ʵ��m��ֵ��P�����ꣻ
��II��������y=f��x����y=g��x����ͼ����������ͬ�Ľ���M��N����ʵ��m��ȡֵ��Χ��
��III���ڣ�II���������£����߶�MN���е���x��Ĵ��߷ֱ���f��x����ͼ���g��x����ͼ����S��T�㣬��S��Ϊ�е���f��x��������l1����TΪ�е���g��x��������l2���Ƿ����ʵ��m��ʹ��l1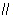 l2��������ڣ����m��ֵ����������ڣ���˵�����ɣ�
l2��������ڣ����m��ֵ����������ڣ���˵�����ɣ�
��I��������y=f��x����y=g��x����ͼ���ڹ�����P������ͬ�����ߣ���ʵ��m��ֵ��P�����ꣻ
��II��������y=f��x����y=g��x����ͼ����������ͬ�Ľ���M��N����ʵ��m��ȡֵ��Χ��
��III���ڣ�II���������£����߶�MN���е���x��Ĵ��߷ֱ���f��x����ͼ���g��x����ͼ����S��T�㣬��S��Ϊ�е���f��x��������l1����TΪ�е���g��x��������l2���Ƿ����ʵ��m��ʹ��l1
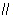 l2��������ڣ����m��ֵ����������ڣ���˵�����ɣ�
l2��������ڣ����m��ֵ����������ڣ���˵�����ɣ��⣺��I���躯��y=f��x����y=g��x��ͼ��Ĺ�����ΪP��x0��y0����
����lnx0=��m+1��x02��x0�٣�
���ڵ�P���й�ͬ�����ߣ�
��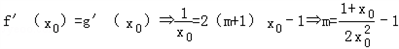 ����
����
�ڴ���٣���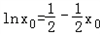 ��
��
��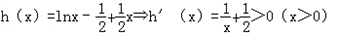 ��
��
���ԣ�����h��x�����ֻ��1����㣬�۲��x0=1����㣬
��m=0��
��ʱ����P��1��0����
��II�����ݣ�I��֪����m=0ʱ�������������ڵ�P��1��0����
��ʱ���仯��y=g��x����ͼ��ĶԳ�����x= ��
��
��y=f��x���ǹ̶�����ģ���������öԳ��������ƶ�����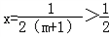 ��
��
��é�1��m��0��
����������������ͬ�Ľ��㣬
��m����1ʱ���������£�ֻ��һ�����㣬��Ȼ�������⣬���ԣ��Щ�1��m��0��
��III���������������m��������M��x1��y1����N��x2��y2������x1��x2��
��MN�е������Ϊ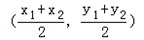 ��
��
��SΪ���ߵ�����l1��б��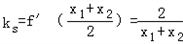 ��
��
��TΪ�е������l2��б��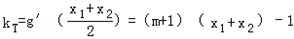 ��
��
�������m��ʹ��ks=kT����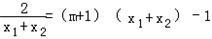 ����
����
������lnx1=��m+1��x12��x1��lnx2=��m+1��x22��x2��
������۵�����ͬ����x1��x2����
��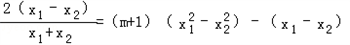 ��
��
��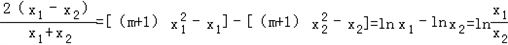 ��
��
Ҳ����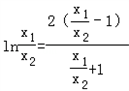 ��
��
���=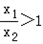 ������
������ ��
��
��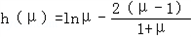 ���̣�1����
���̣�1����
��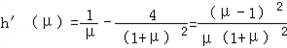 ��
��
�ߦ̣�1��
��h'���̣���0����ˣ�h���̣���[1��+��]�ϵ���������
��h���̣���h��1��=0��
��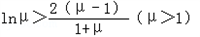 ��
��
������ì�ܣ�
���ԣ�������ʵ��mʹ��l1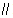 l2��
l2��
����lnx0=��m+1��x02��x0�٣�
���ڵ�P���й�ͬ�����ߣ�
��
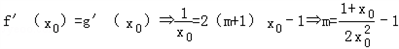 ����
�����ڴ���٣���
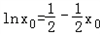 ��
����
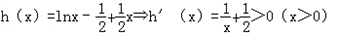 ��
�����ԣ�����h��x�����ֻ��1����㣬�۲��x0=1����㣬
��m=0��
��ʱ����P��1��0����
��II�����ݣ�I��֪����m=0ʱ�������������ڵ�P��1��0����
��ʱ���仯��y=g��x����ͼ��ĶԳ�����x=
 ��
����y=f��x���ǹ̶�����ģ���������öԳ��������ƶ�����
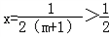 ��
����é�1��m��0��
����������������ͬ�Ľ��㣬
��m����1ʱ���������£�ֻ��һ�����㣬��Ȼ�������⣬���ԣ��Щ�1��m��0��
��III���������������m��������M��x1��y1����N��x2��y2������x1��x2��
��MN�е������Ϊ
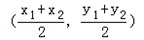 ��
����SΪ���ߵ�����l1��б��
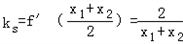 ��
����TΪ�е������l2��б��
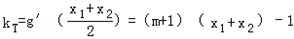 ��
���������m��ʹ��ks=kT����
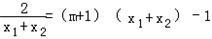 ����
����������lnx1=��m+1��x12��x1��lnx2=��m+1��x22��x2��
������۵�����ͬ����x1��x2����
��
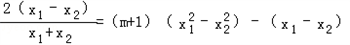 ��
����
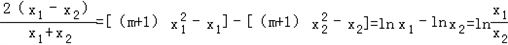 ��
��Ҳ����
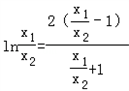 ��
�����=
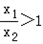 ������
������ ��
����
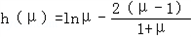 ���̣�1����
���̣�1������
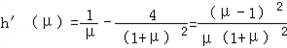 ��
���ߦ̣�1��
��h'���̣���0����ˣ�h���̣���[1��+��]�ϵ���������
��h���̣���h��1��=0��
��
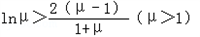 ��
��������ì�ܣ�
���ԣ�������ʵ��mʹ��l1
 l2��
l2��
��ϰ��ϵ�д�
 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
�����Ŀ