题目内容
设 都是锐角,且
都是锐角,且 ,
, ,则
,则 =( )
=( )
 都是锐角,且
都是锐角,且 ,
, ,则
,则 =( )
=( )A. | B. | C. 或 或 | D. 或 或 |
B
试题分析:由α、β都是锐角,且cosα值小于
 ,得到sinα大于0,利用余弦函数的图象与性质得出α的范围,再由sin(α+β)的值大于
,得到sinα大于0,利用余弦函数的图象与性质得出α的范围,再由sin(α+β)的值大于 ,利用正弦函数的图象与性质得出α+β为钝角,可得出cos(α+β)小于0,然后利用同角三角函数间的基本关系分别求出sinα和cos(α+β)的值,将所求式子中的角β变形为(α+β)-α,利用两角和与差的余弦函数公式化简后,把各自的值代入即可求出值.解:∵α、β都是锐角,且cosα=
,利用正弦函数的图象与性质得出α+β为钝角,可得出cos(α+β)小于0,然后利用同角三角函数间的基本关系分别求出sinα和cos(α+β)的值,将所求式子中的角β变形为(α+β)-α,利用两角和与差的余弦函数公式化简后,把各自的值代入即可求出值.解:∵α、β都是锐角,且cosα=
<
 ,∴
,∴ <α<
<α< ,又sin(α+β)=
,又sin(α+β)= ∴
∴ <α+β<π,∴cos(α+β)=-
<α+β<π,∴cos(α+β)=- ,sinα=
,sinα=
则cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-
 故选B
故选B点评:此题考查了同角三角函数间的基本关系,正弦、余弦函数的图象与性质,以及两角和与差的余弦函数公式,熟练掌握公式及基本关系是解本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 ( )
( )



 ,且
,且
 的值.
的值. 的值.
的值. ,则( )
,则( )
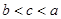


 ,θ为第二象限角,则tan2θ=______
,θ为第二象限角,则tan2θ=______ ,则
,则




 ,
, ,其中
,其中 .
. ;(2)求
;(2)求 的值.
的值. ( )
( )


 则
则 ( )
( )


