题目内容
设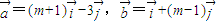 ,其中
,其中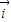 ,
, 为互相垂直的单位向量,又
为互相垂直的单位向量,又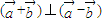 ,则实数m= .
,则实数m= .
【答案】分析:利用向量坐标的定义写出两个向量的坐标,利用向量垂直的充要条件列出方程,利用向量模的坐标公式,将方程中向量的模用坐标表示,得到关于m的方程,解方程求出m的值.
解答:解:∵ ,其中
,其中 为互相垂直的单位向量
为互相垂直的单位向量
∴ ,
,
∵
∴
∴
∴(m+1)2+9=1+(m-1)2
解得m=-2
故答案为:-2.
点评:解决向量垂直的问题,利用向量垂直的充要条件:数量积为0,列出方程解决;解决向量的模问题常利用向量模的平方等于向量的平方处理.
解答:解:∵
 ,其中
,其中 为互相垂直的单位向量
为互相垂直的单位向量∴
 ,
,
∵

∴

∴

∴(m+1)2+9=1+(m-1)2
解得m=-2
故答案为:-2.
点评:解决向量垂直的问题,利用向量垂直的充要条件:数量积为0,列出方程解决;解决向量的模问题常利用向量模的平方等于向量的平方处理.

练习册系列答案
相关题目
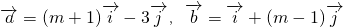 ,其中
,其中 ,
, 为互相垂直的单位向量,又
为互相垂直的单位向量,又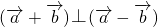 ,则实数m=________.
,则实数m=________.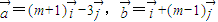 ,其中
,其中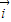 ,
, 为互相垂直的单位向量,又
为互相垂直的单位向量,又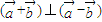 ,则实数m= .
,则实数m= .