题目内容
如图，已知O为△ABC的外心，a，b，c分别是角A、B、C的对边，且满足| CO |
| AB |
| BO |
| CA |
（Ⅰ）证明：2a2=b2+c2；
（Ⅱ）求
| tanA |
| tanB |
| tanA |
| tanC |
分析：（Ⅰ）取AB、AC的中点E、F，则根据三角形法则可得：
•
=
(
+
)•(
-
)=
(a2-b2)，同理
•
=
(c2-a2)；进而得到答案．
（Ⅱ）由题意可得：
+
=(
+
)•
，再结合两角和与差的正余弦公式、正弦定理、余弦定理进行化简即可求出答案．
| CO |
| AB |
| 1 |
| 2 |
| CB |
| CA |
| CB |
| CA |
| 1 |
| 2 |
| BO |
| CA |
| 1 |
| 2 |
（Ⅱ）由题意可得：
| tanA |
| tanB |
| tanA |
| tanC |
| cosB |
| sinB |
| cosC |
| sinC |
| sinA |
| cosA |
解答：解：（Ⅰ）取AB、AC的中点E、F，
则
•
=(
+
)•
=
•
=
(
+
)•(
-
)=
(a2-b2)…（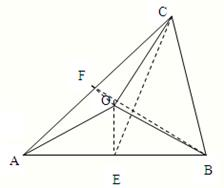
3分）
同理
•
=
(c2-a2)；
所以2a2=b2+c2．…（5分）
（Ⅱ）由题意可得：
+
=(
+
)•
=
=
=2…（10分）
则
| CO |
| AB |
| CE |
| EO |
| AB |
| CE |
| AB |
| 1 |
| 2 |
| CB |
| CA |
| CB |
| CA |
| 1 |
| 2 |
3分）同理
| BO |
| CA |
| 1 |
| 2 |
所以2a2=b2+c2．…（5分）
（Ⅱ）由题意可得：
| tanA |
| tanB |
| tanA |
| tanC |
| cosB |
| sinB |
| cosC |
| sinC |
| sinA |
| cosA |
=
| sin(B+C)•sinA |
| sinB•sinC•cosA |
| a2 | ||
bc•
|
点评：夹角此类问题的关键是熟练掌握向量的三角形法则，以及解三角形的正弦定理与余弦定理等有关三角形的常用知识点．
练习册系列答案
相关题目
（2011•海淀区二模）如图，已知⊙O的弦AB交半径OC于点D，若AD=3，BD=2，且D为OC的中点，则CD的长为
如图，已知O为△ABC的外心，a，b，c分别是角A、B、C的对边，且满足
+
+
=0是O为△ABC的重心的充要条件．
??