题目内容
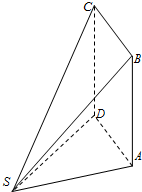 如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=1,AB=2,SD=
如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=1,AB=2,SD=| 3 |
(1)求证:CD⊥平面ADS;
(2)求二面角A-SB-D的余弦值.
(3)求点A到面SBC的距离.
分析:(1)要证CD⊥平面ADS,只需证明直线CD垂直平面ADS内的两条相交直线AD、SD即可;
(2)过A作AE⊥DB于E 又过A作AF⊥SB于F,连接EF,可得∠AFB为二面角A-SB-D的平面角,解三角形可求二面角A-SB-D的余弦值;
(3)根据AD∥BC,可得点A到面SBC的距离等于点D到面SBC的距离,从而可得结论.
(2)过A作AE⊥DB于E 又过A作AF⊥SB于F,连接EF,可得∠AFB为二面角A-SB-D的平面角,解三角形可求二面角A-SB-D的余弦值;
(3)根据AD∥BC,可得点A到面SBC的距离等于点D到面SBC的距离,从而可得结论.
解答:(1)证明:∵ABCD是矩形,∴CD⊥AD
又SD⊥AB,AB∥CD,则CD⊥SD
又∵AD∩SD=D
∴CD⊥平面ADS
(2)解:∵△SAD中SD⊥AD,且SD⊥AB,AB∩AD=A
∴SD⊥面ABCD.
∴平面SDB⊥平面ABCD,BD为面SDB与面ABCD的交线.
过A作AE⊥DB于E,则AE⊥平面SDB,过A作AF⊥SB于F,连接EF,从而得:EF⊥SB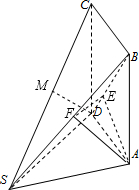
∴∠AFB为二面角A-SB-D的平面角
在矩形ABCD中,对角线BD=
∴在△ABD中,AE=
=
Rt△SDC中,SC=
,Rt△SBC,SB=
而Rt△SAD中,SA=2,且AB=2,∴SB2=SA2+AB2,
∴△SAB为等腰直角三角形且∠SAB为直角,
∴AF=
AB=2
∴sin∠AFE=
=
∴所求的二面角的余弦值为
;
(3)解:∵AD∥BC,∴点A到面SBC的距离等于点D到面SBC的距离
∵SD⊥面ABCD,BC?面ABCD,∴SD⊥BC
∵BC⊥CD,SD∩CD=D,∴BC⊥平面SDC
∴平面SBC⊥平面SDC
过D作DM⊥SC,垂足为M,则DM⊥平面SBC,即DM为点D到面SBC的距离
在△SDC中,SD=
,CD=2,∴SC=
,
∴DM=
=
.
又SD⊥AB,AB∥CD,则CD⊥SD
又∵AD∩SD=D
∴CD⊥平面ADS
(2)解:∵△SAD中SD⊥AD,且SD⊥AB,AB∩AD=A
∴SD⊥面ABCD.
∴平面SDB⊥平面ABCD,BD为面SDB与面ABCD的交线.
过A作AE⊥DB于E,则AE⊥平面SDB,过A作AF⊥SB于F,连接EF,从而得:EF⊥SB

∴∠AFB为二面角A-SB-D的平面角
在矩形ABCD中,对角线BD=
| 5 |
∴在△ABD中,AE=
| AB•CD |
| BD |
2
| ||
| 5 |
Rt△SDC中,SC=
| 7 |
| 8 |
而Rt△SAD中,SA=2,且AB=2,∴SB2=SA2+AB2,
∴△SAB为等腰直角三角形且∠SAB为直角,
∴AF=
| ||
| 2 |
∴sin∠AFE=
| AE |
| AF |
| ||
| 5 |
∴所求的二面角的余弦值为
| ||
| 5 |
(3)解:∵AD∥BC,∴点A到面SBC的距离等于点D到面SBC的距离
∵SD⊥面ABCD,BC?面ABCD,∴SD⊥BC
∵BC⊥CD,SD∩CD=D,∴BC⊥平面SDC
∴平面SBC⊥平面SDC
过D作DM⊥SC,垂足为M,则DM⊥平面SBC,即DM为点D到面SBC的距离
在△SDC中,SD=
| 3 |
| 7 |
∴DM=
| SD×DC |
| SC |
2
| ||
| 7 |
点评:本题考查线面垂直,考查面面角,考查点面距离的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


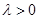 使得
使得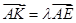 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为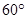 ,求
,求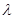 的值。
的值。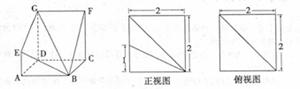
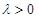 使得
使得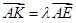 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为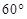 ,求
,求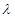 的值。
的值。
 使得
使得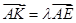 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为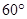 ,求
,求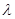 的值。
的值。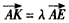 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。