题目内容
平面内动点M与点P1(-2,0),P2(2,0)所成直线的斜率分别为k1、k2,且满足k1k2=-
.
(1)求点M的轨迹E的方程,并指出E的曲线类型;
(2)设直线l:y=kx+m(k>0,m≠0)分别交x、y 轴于点A、B,交曲线E于点C、D,且|AC|=|BD|,N(
,1)求k的值及△NCD面积取得最大时直线l的方程.
| 1 |
| 2 |
(1)求点M的轨迹E的方程,并指出E的曲线类型;
(2)设直线l:y=kx+m(k>0,m≠0)分别交x、y 轴于点A、B,交曲线E于点C、D,且|AC|=|BD|,N(
| 2 |
分析:(1)设动点M的坐标为(x,y),由k1•k2=-
,可得
•
=-
,整理可求
(2)在l:y=kx+m中分别令x=0,y=0可得A(-
,0),B(0,m),从而可得AB的中点为Q(-
,
),联立方程结合方程的根与系数的关系及|AC|=|BD|,可得CD中点就是AB中点,从而可求k,由于CD|=
•|x2-x1|=
•
=
•
=
,点N到CD的距离d=
=
|m|,代入利用基本不等式可求面积的最大值及K的值,进而可求直线方程
| 1 |
| 2 |
| y |
| x+2 |
| y |
| x-2 |
| 1 |
| 2 |
(2)在l:y=kx+m中分别令x=0,y=0可得A(-
| m |
| k |
| m |
| 2k |
| m |
| 2 |
| 1+k2 |
1+
|
| (x1+x2)2-4x1x2 |
|
| 2m2-4(m2-2) |
| 3(4-m2) |
|
| ||
|
| ||
| 3 |
解答:解:(1)设动点M的坐标为(x,y),∵k1•k2=-
,∴
•
=-
,即
+
=1(y≠0)
动点M的轨迹E是中心在原点,半长轴为2,焦点为(±
,0)的椭圆
(除去长轴两个端点.) 它的方程是
+
=1(y≠0).
(2)在l:y=kx+m中分别令x=0,y=0可得A(-
,0),B(0,m),AB的中点为Q(-
,
)
设C(x1,y1),D(x2,y2),由
⇒(1+2k2)x2+4mkx+2m2-4=0△=32k2-8m2+16,x1+x2=-
,x1•x2=
,
∵|AC|=|BD|,∴CD中点就是AB中点,
即-
=-
,4k2=1+2k2,k2=
,∵k>0,∴k=
(2)|CD|=
•|x2-x1|=
•
=
•
=
点N到CD的距离d=
=
|m|,S△NCD=
|CD|•d=
•
•
|m|=
≤
(4-m2+m2)=2
当且仅当4-m2=m2时等号成立,即m2=2,m=±
,此时△>0,
所以直线的方程为l:y=
x±
.
| 1 |
| 2 |
| y |
| x+2 |
| y |
| x-2 |
| 1 |
| 2 |
| x2 |
| 4 |
| y2 |
| 2 |
动点M的轨迹E是中心在原点,半长轴为2,焦点为(±
| 2 |
(除去长轴两个端点.) 它的方程是
| x2 |
| 4 |
| y2 |
| 2 |
(2)在l:y=kx+m中分别令x=0,y=0可得A(-
| m |
| k |
| m |
| 2k |
| m |
| 2 |
设C(x1,y1),D(x2,y2),由
|
| 4mk |
| 1+2k2 |
| 2m2-4 |
| 1+2k2 |
∵|AC|=|BD|,∴CD中点就是AB中点,
即-
| 4mk |
| 1+2k2 |
| m |
| k |
| 1 |
| 2 |
| ||
| 2 |
| 1+k2 |
1+
|
| (x1+x2)2-4x1x2 |
|
| 2m2-4(m2-2) |
| 3(4-m2) |
点N到CD的距离d=
|
| ||
|
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3(4-m2) |
| ||
| 3 |
| ||
| 2 |
| (4-m2)m2 |
| ||
| 2 |
| 2 |
当且仅当4-m2=m2时等号成立,即m2=2,m=±
| 2 |
所以直线的方程为l:y=
| ||
| 2 |
| 2 |
点评:本题主要考查了利用直线的斜率关系求解点的轨迹方程,要注意(1)中要去掉不符合条件的点,考查了基本不等式在求解最值中的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
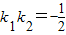 .
.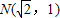 ,求△NCD面积取得最大时直线l的方程.
,求△NCD面积取得最大时直线l的方程. .
. 求k的值及△NCD面积取得最大时直线l的方程.
求k的值及△NCD面积取得最大时直线l的方程.