题目内容
设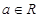 ,函数
,函数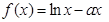 .
.
(1) 若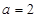 ,求曲线
,求曲线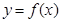 在
在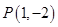 处的切线方程;
处的切线方程;
(2) 若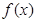 无零点,求实数
无零点,求实数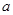 的取值范围;
的取值范围;
(3) 若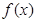 有两个相异零点
有两个相异零点 ,求证:
,求证: 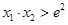 .
.
解:方法一在区间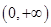 上,
上,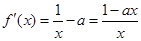 .
……………………1分
.
……………………1分
(1)当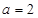 时,
时,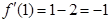 ,则切线方程为
,则切线方程为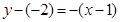 ,即
,即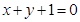 …………3分
…………3分
(2)①若 ,则
,则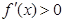 ,
,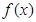 是区间
是区间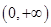 上的增函数,
上的增函数,
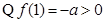 ,
,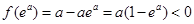 ,
,
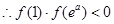 ,函数
,函数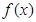 在区间
在区间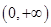 有唯一零点.
…………6分
有唯一零点.
…………6分
②若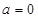 ,
,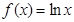 有唯一零点
有唯一零点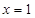 .
…………7分
.
…………7分
③若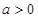 ,令
,令 得:
得:  .
.
在区间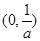 上,
上, 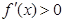 ,函数
,函数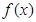 是增函数;
是增函数;
在区间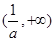 上,
上,  ,函数
,函数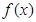 是减函数;
是减函数;
故在区间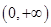 上,
上, 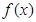 的极大值为
的极大值为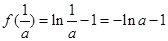 .
.
由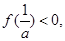 即
即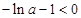 ,解得:
,解得: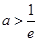 .
.
故所求实数a的取值范围是 .
…………9分
.
…………9分
方法二、函数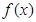 无零点
无零点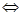 方程
方程 即
即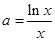 在
在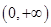 上无实数解 …………4分
上无实数解 …………4分
令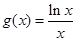 ,则
,则
由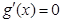 即
即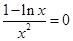 得:
得: …………6分
…………6分
在区间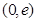 上,
上,  ,函数
,函数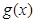 是增函数;
是增函数;
在区间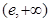 上,
上,  ,函数
,函数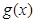 是减函数;
是减函数;
故在区间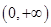 上,
上, 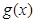 的极大值为
的极大值为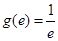 .
…………7分
.
…………7分
注意到 时,
时,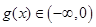 ;
;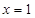 时
时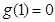 ;
;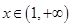 时,
时,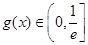
故方程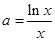 在
在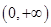 上无实数解
上无实数解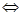
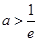 .
.
即所求实数a的取值范围是 .
…………9分
.
…………9分
[注:解法二只说明了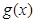 的值域是
的值域是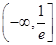 ,但并没有证明.]
,但并没有证明.]
(3) 设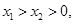
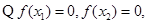
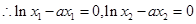
 ,
,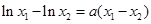
原不等式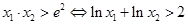
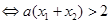


令 ,则
,则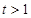 ,于是
,于是 .
…………12分
.
…………12分
设函数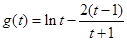
 ,
,
求导得: 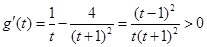
故函数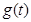 是
是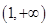 上的增函数,
上的增函数, 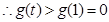
即不等式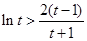 成立,故所证不等式
成立,故所证不等式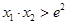 成立.
……………………14分
成立.
……………………14分
【解析】略

 春雨教育同步作文系列答案
春雨教育同步作文系列答案