题目内容
对于所有实数x,不等式x2+|2x-4|≥a恒成立,则实数a的最大值是________.
4
分析:欲求不等式x2+|2x-4|≥a对于一切实数x均成立,只需求f(x)=x2+|2x-4|的最小值即可,根据分段函数的性质求出最小值,即可求出a的最大值.
解答:要求不等式x2+|2x-4|≥a对于一切实数x均成立,
只需求f(x)=x2+|2x-4|的最小值
f(x)=x2+|2x-4|=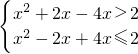
∴根据分段函数的意义可知f(x)≥f(2)=4
即a≤4
故答案为:4.
点评:本题主要考查了函数恒成立,以及绝对值不等式和分段函数的最值,属于基础题.
分析:欲求不等式x2+|2x-4|≥a对于一切实数x均成立,只需求f(x)=x2+|2x-4|的最小值即可,根据分段函数的性质求出最小值,即可求出a的最大值.
解答:要求不等式x2+|2x-4|≥a对于一切实数x均成立,
只需求f(x)=x2+|2x-4|的最小值
f(x)=x2+|2x-4|=
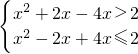
∴根据分段函数的意义可知f(x)≥f(2)=4
即a≤4
故答案为:4.
点评:本题主要考查了函数恒成立,以及绝对值不等式和分段函数的最值,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
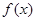 =x3+ax2-x+1,给出下列命题:
=x3+ax2-x+1,给出下列命题: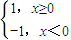 则f1(x)∈M;
则f1(x)∈M;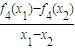 <0成立.
<0成立.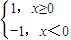 则f1(x)∈M;
则f1(x)∈M;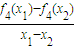 <0成立.
<0成立.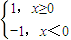 则f1(x)∈M;
则f1(x)∈M;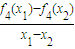 <0成立.
<0成立.