题目内容
已知椭圆 (
( )的右焦点为
)的右焦点为 ,离心率为
,离心率为 .
.
(Ⅰ)若 ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)设直线 与椭圆相交于
与椭圆相交于 ,
, 两点,
两点, 分别为线段
分别为线段 的中点. 若坐标原点
的中点. 若坐标原点 在以
在以 为直径的圆上,且
为直径的圆上,且 ,求
,求 的取值范围.
的取值范围.
 (
( )的右焦点为
)的右焦点为 ,离心率为
,离心率为 .
.(Ⅰ)若
 ,求椭圆的方程;
,求椭圆的方程;(Ⅱ)设直线
 与椭圆相交于
与椭圆相交于 ,
, 两点,
两点, 分别为线段
分别为线段 的中点. 若坐标原点
的中点. 若坐标原点 在以
在以 为直径的圆上,且
为直径的圆上,且 ,求
,求 的取值范围.
的取值范围.(Ⅰ)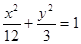 ;(Ⅱ)
;(Ⅱ)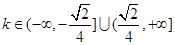
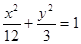 ;(Ⅱ)
;(Ⅱ)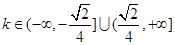
试题分析:(Ⅰ)由已知椭圆的半焦距
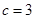 ,又
,又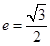 ,根据离心率的定义得
,根据离心率的定义得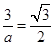 ,则
,则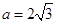 ,所以
,所以 ,从而得出所求椭圆的方程为
,从而得出所求椭圆的方程为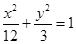 .
.(2)根据题意可设点
 、
、 的坐标分别为
的坐标分别为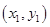 、
、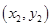 ,联立直线方程
,联立直线方程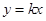 与椭圆方程
与椭圆方程 ,消去
,消去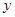 得
得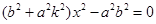 ,则
,则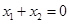 ,
,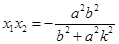 ,因为原点
,因为原点 在圆上,所以
在圆上,所以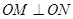 ,根据三角形中位线性质可知四边形
,根据三角形中位线性质可知四边形 为矩形,所以
为矩形,所以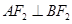 ,又
,又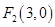 ,所以
,所以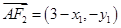 ,
,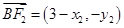 ,因此
,因此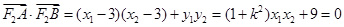 ,即
,即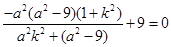 ,从而可整理得
,从而可整理得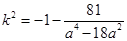 ,又因为
,又因为 ,所以
,所以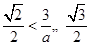 ,即
,即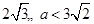 ,从而
,从而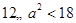 ,所以
,所以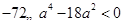 ,因此
,因此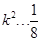 ,解得
,解得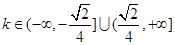 .(如图所示)
.(如图所示)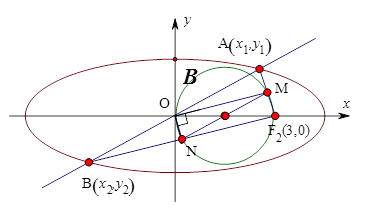
试题解析:(Ⅰ)由题意得
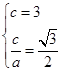 ,得
,得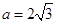 . 2分
. 2分结合
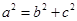 ,解得
,解得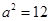 ,
,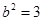 . 3分
. 3分所以,椭圆的方程为
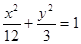 . 4分
. 4分(Ⅱ)由
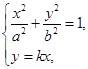 得
得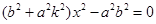 .
. 设
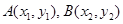 .
.所以, 6分
依题意,
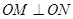 ,
,易知,四边形
 为平行四边形,
为平行四边形,所以
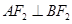 , 7分
, 7分因为
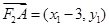 ,
,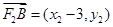 ,
,所以
 . 8分
. 8分即
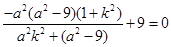 , 9分
, 9分将其整理为
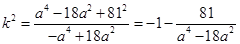 . 10分
. 10分因为
 ,所以
,所以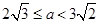 ,
, . 11分
. 11分所以
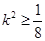 ,即
,即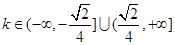 . 13分
. 13分
练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目

 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
 上的点到其两焦点距离之和为
上的点到其两焦点距离之和为 ,且过点
,且过点 .
.  为坐标原点,斜率为
为坐标原点,斜率为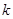 的直线过椭圆的右焦点,且与椭圆交于点
的直线过椭圆的右焦点,且与椭圆交于点 ,
,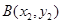 ,若
,若 ,求△
,求△ 的面积.
的面积. ,直线AM、BM相交于点M,且这两条直线的斜率之积为
,直线AM、BM相交于点M,且这两条直线的斜率之积为 .
. (
( )相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
)相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R. 经过点
经过点 ,离心率为
,离心率为 .
. 的两个焦点为F1,F2,椭圆上一点M
的两个焦点为F1,F2,椭圆上一点M
 .
. 与椭圆恒有不同交点A,B,且
与椭圆恒有不同交点A,B,且 (O为坐标原点),求实数k的范围.
(O为坐标原点),求实数k的范围.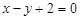 与曲线
与曲线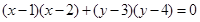 的交点个数是 .
的交点个数是 .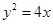 焦点
焦点 的直线
的直线 与抛物线相交于
与抛物线相交于 两点,若
两点,若 ,则
,则 .
.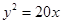 的焦点为圆心,且与双曲线
的焦点为圆心,且与双曲线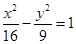 的两条渐近线都相切的圆的方程为 .
的两条渐近线都相切的圆的方程为 .