题目内容
设函数f(x)=x2-4x+3,g(x)=3x-2,集合M={x∈R|f(g(x))>0},N={x∈R|g(x)<2},则M∩N为( )
| A.(1,+∞) | B.(0,1) |
| C.(-1,1) | D.(-∞,1) |
D
M:f(g(x))=(3x-2)2-4(3x-2)+3>0,
令t=3x-2,则原不等式等价于t2-4t+3>0,解得t>3或t<1,
∴3x-2>3或3x-2<1.
∴3x>5或3x<3.
∴x>log35或x<1.
即M={x|x>log35或x<1}.
N:3x-2<2⇒3x<4⇒x<log34,
∴N={x|x<log34},
∴M∩N={x|x<1},故选D.
令t=3x-2,则原不等式等价于t2-4t+3>0,解得t>3或t<1,
∴3x-2>3或3x-2<1.
∴3x>5或3x<3.
∴x>log35或x<1.
即M={x|x>log35或x<1}.
N:3x-2<2⇒3x<4⇒x<log34,
∴N={x|x<log34},
∴M∩N={x|x<1},故选D.

练习册系列答案
相关题目
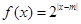 和函数
和函数 ,其中
,其中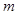 为参数,且满足
为参数,且满足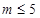 .
.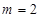 ,写出函数
,写出函数 的单调区间(无需证明);
的单调区间(无需证明);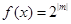 在
在 上有唯一解,求实数
上有唯一解,求实数 ,存在
,存在 ,使得
,使得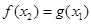 成立,求实数
成立,求实数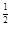 ,b=log
,b=log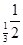 ,c=log
,c=log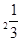 ,则( )
,则( )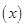 =2x
=2x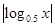 -1的零点个数是________.
-1的零点个数是________.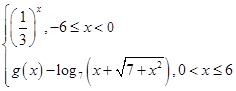 若f(x)是奇函数,则g(3)=________.
若f(x)是奇函数,则g(3)=________.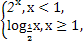 则函数f(1-x)的图象是( )
则函数f(1-x)的图象是( )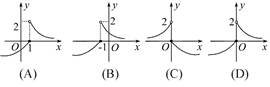
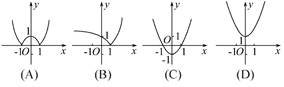
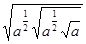 的结果为( )
的结果为( )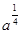


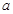
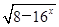 的定义域是________.
的定义域是________.