题目内容
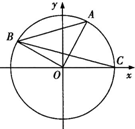 如图A.B是单位圆O上的点,且点B在第二象限. C是圆O与x轴正半轴的交点,A点的坐标为(
如图A.B是单位圆O上的点,且点B在第二象限. C是圆O与x轴正半轴的交点,A点的坐标为(| 3 |
| 5 |
| 4 |
| 5 |
(1)求sin∠COA;
(2)求BC的长度.
分析:(1)根据三角函数的定义可直接得到答案.
(2)可由两角和的正、余弦定理先求出点B的坐标,再根据两点间的距离公式可得答案.
(2)可由两角和的正、余弦定理先求出点B的坐标,再根据两点间的距离公式可得答案.
解答:解:(1)因为A点的坐标为(
,
),根据三角函数的定义可知sin∠COA=
(2)因为三角形AOB为直角三角形,所以∠AOB=90°
sin∠COA=
,cos∠COA=
所以cos∠COB=cos(
+∠AOC)=-sin∠AOC=-
sin∠BOC=sin(
+∠AOC)=cos∠AOC=
解法1:|BC|2=|OC|2+|OB|2-2|OC||OB|cos∠BOC=
|BC|=
解法2:由定义知A(
,
) B=(-
,
)
由两点间的距离公式得|BC|=
=
|BC|=
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
(2)因为三角形AOB为直角三角形,所以∠AOB=90°
sin∠COA=
| 4 |
| 5 |
| 3 |
| 5 |
所以cos∠COB=cos(
| π |
| 2 |
| 4 |
| 5 |
sin∠BOC=sin(
| π |
| 2 |
| 3 |
| 5 |
解法1:|BC|2=|OC|2+|OB|2-2|OC||OB|cos∠BOC=
| 18 |
| 5 |
|BC|=
| 3 |
| 5 |
| 10 |
解法2:由定义知A(
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
由两点间的距离公式得|BC|=
| 90 |
| 25 |
| 18 |
| 5 |
|BC|=
| 3 |
| 5 |
| 10 |
点评:本题主要考查三角函数的定义以及余弦定理.这种题型是高考必考题型.

练习册系列答案
相关题目
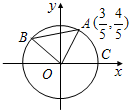 如图A,B是单位圆O上的点,且B在第二象限. C是圆与x轴正半轴的交点,A点的坐标为
如图A,B是单位圆O上的点,且B在第二象限. C是圆与x轴正半轴的交点,A点的坐标为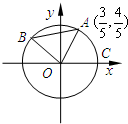 如图A、B是单位圆O上的点,且B在第二象限.C是圆与x轴正半轴的交点,A点的坐标为(
如图A、B是单位圆O上的点,且B在第二象限.C是圆与x轴正半轴的交点,A点的坐标为( 如图A,B是单位圆O上的点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形.若A点的坐标为(
如图A,B是单位圆O上的点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形.若A点的坐标为(