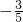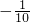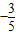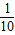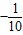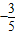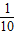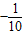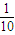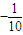Question

设-5＜a＜5，集合M={x∈N|2^x-（a+5）x-10=0}．若M≠?，则满足条件的所有实数a的和等于（　　）

• A．-

  3

  5

• B．4
• C．

  1

  10

• D．-

  1

  10

Answer 1

分析：先由条件判断x≥4，由于函数的导数大于零，可得f（x）在x≥4时单调增，故至多只有一个零点．分别令f（4）=0、
f（5）=0、f（6）=0、f（7）=0，求得a的值，x≥7时，f（x）恒大于0，不会有零点．最后把求得的a值相加，即得所求．

解答：解：因-5＜a＜5，x为自然数，且2^x=（a+5）x+10≥10，∴x≥4．
令f（x）=2^x-（a+5）x-10 得：f'（x）=2^x ln2-（a+5）≥16ln2-（a+5）＞0，
即f（x）在x≥4时单调增，故至多只有一个零点．
令f（4）=6-4（a+5）=0，解得 a=-3.5；
f（5）=22-5（a+5）=0，解得：a=-0.6；
f（6）=54-6（a+5）=0，得：a=4；
f（7）=118-7（a+5）＞0，x≥7时，f（x）恒大于0，不会有零点．
因此满足条件的a有3个，其和为-3.5-0.6+4=-0.1，
故选D．

点评：本题考查了根的存在性及根的个数判断，求函数的导数，属于中档题．