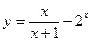题目内容
求下列函数的导函数:
(1)y=2x+lnx
(2)y=2xcosx
(3)y=
-2x.
(1)y=2x+lnx
(2)y=2xcosx
(3)y=
| x | x+1 |
分析:(1)直接利用和的导数等于导数的和展开;
(2)直接利用乘积的导数的运算法则展开;
(3)利用商的导数的运算法则进行展开即可.
(2)直接利用乘积的导数的运算法则展开;
(3)利用商的导数的运算法则进行展开即可.
解答:解:(1)由y=2x+lnx,则y′=(2x+lnx)′=2+
;
(2)由y=2xcosx,则y′=(2xcosx)′=2cosx-2xsinx;
(3)由3)y=
-2x,则y′=(
-2x)′=
-2xln2=
-2xln2.
| 1 |
| x |
(2)由y=2xcosx,则y′=(2xcosx)′=2cosx-2xsinx;
(3)由3)y=
| x |
| x+1 |
| x |
| x+1 |
| x′•(x+1)-x•(x+1)′ |
| (x+1)2 |
| 1 |
| (x+1)2 |
点评:本题考查了导数的运算,分别考查了和的导数,乘积的导数和商的导数的运算法则,考查了基本初等函数的求导公式,是基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
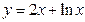 (2)
(2)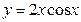 (3)
(3)