ΧβΡΩΡΎ»ί
Φ«Κ· ΐfn(x)=a•xn-1(aΓ RΘ§nΓ N*)ΒΡΒΦΚ· ΐΈΣ
(x)Θ§“―÷Σ
(2)=12Θ°
Θ®ΔώΘ©«σaΒΡ÷ΒΘ°
Θ®ΔρΘ©…ηΚ· ΐgn(x)=fn(x)-n2InxΘ§ ‘Έ ΘΚ «Ζώ¥φ‘Ύ’ΐ’ϊ ΐn ΙΒΟΚ· ΐgnΘ®xΘ©”–«“÷Μ”–“ΜΗωΝψΒψΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΥυ”–nΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Θ®ΔσΘ©»τ Β ΐx0ΚΆmΘ®mΘΨ0Θ§«“mΓΌ1Θ©¬ζΉψΘΚ
=
Θ§ ‘±»Ϋœx0”κmΒΡ¥σ–ΓΘ§≤ΔΦ”“‘÷ΛΟςΘ°
| f | Γδ n |
| f | Γδ 3 |
Θ®ΔώΘ©«σaΒΡ÷ΒΘ°
Θ®ΔρΘ©…ηΚ· ΐgn(x)=fn(x)-n2InxΘ§ ‘Έ ΘΚ «Ζώ¥φ‘Ύ’ΐ’ϊ ΐn ΙΒΟΚ· ΐgnΘ®xΘ©”–«“÷Μ”–“ΜΗωΝψΒψΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΥυ”–nΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Θ®ΔσΘ©»τ Β ΐx0ΚΆmΘ®mΘΨ0Θ§«“mΓΌ1Θ©¬ζΉψΘΚ
| ||
|
| fn(m) |
| fn+1(m) |
Ζ÷ΈωΘΚΘ®ΔώΘ©÷±Ϋ””…
(2)=12Ν– Ϋ«σaΒΡ÷ΒΘΜ
Θ®ΔρΘ©«σ≥ωΚ· ΐΒΡΒΦΚ· ΐΘ§«σ≥ωΒΦΚ· ΐΒΡΝψΒψΘ§”…ΒΦΚ· ΐΒΡΝψΒψΕ‘Ε®“ε”ρΖ÷ΕΈΘ§”…ΒΦΚ· ΐΒΡΖϊΚ≈≈–Εœ‘≠Κ· ΐΒΡΒΞΒς–‘Θ§«σ≥ω‘≠Κ· ΐΒΡΉν÷ΒΘ§ΗυΨίΉν÷ΒΖ÷ΈωΚ· ΐΒΡΝψΒψΗω ΐΘΜ
Θ®ΔσΘ©«σ≥ωfnΓδ(x)=n•xn-1Θ§¥ζ»κ
=
Θ§Ϋβ≥ωx0Θ§Α―x0”κmΉς≤νΚσΙΙ‘λΗ®÷ζΚ· ΐΘ§«σ≥ωΗ®÷ζΚ· ΐΒΡΒΦΚ· ΐΘ§”…Η®÷ζΚ· ΐΒΡΒΞΒς–‘Φ¥Ω…÷ΛΟςx0”κmΒΡ≤ν”κ0ΒΡ¥σ–ΓΙΊœΒΘ§‘ρΫα¬έΒΟΒΫ÷ΛΟςΘ°
| f | Γδ 3 |
Θ®ΔρΘ©«σ≥ωΚ· ΐΒΡΒΦΚ· ΐΘ§«σ≥ωΒΦΚ· ΐΒΡΝψΒψΘ§”…ΒΦΚ· ΐΒΡΝψΒψΕ‘Ε®“ε”ρΖ÷ΕΈΘ§”…ΒΦΚ· ΐΒΡΖϊΚ≈≈–Εœ‘≠Κ· ΐΒΡΒΞΒς–‘Θ§«σ≥ω‘≠Κ· ΐΒΡΉν÷ΒΘ§ΗυΨίΉν÷ΒΖ÷ΈωΚ· ΐΒΡΝψΒψΗω ΐΘΜ
Θ®ΔσΘ©«σ≥ωfnΓδ(x)=n•xn-1Θ§¥ζ»κ
| ||
|
| fn(m) |
| fn+1(m) |
Ϋβ¥πΘΚΫβΘΚΘ®ΔώΘ©f3Γδ(x)=3ax2Θ§”…f3Γδ(2)=12Θ§ΒΟa=1ΘΜ
Θ®ΔρΘ©gn(x)=xn-n2lnx-1Θ§gnΓδ(x)=n•xn-1-
=
Θ§
ΓΏxΘΨ0Θ§ΝνgnΓδ(x)=0Θ§ΒΟx=
Θ°
Β±xΘΨ
±Θ§gnΓδ(x)ΘΨ0Θ§gnΘ®xΘ© «‘ωΚ· ΐΘΜ
Β±0ΘΦxΘΦ
±Θ§gnΓδ(x)ΘΦ0Θ§gnΘ®xΘ© «ΦθΚ· ΐΘΜ
Υυ“‘Β±x=
±Θ§gnΘ®xΘ©”–ΦΪ–Γ÷ΒΘ§“≤ «Ήν–Γ÷ΒΘ§gn(
)=n-nlnn-1Θ°
Β±xΓζ0 ±Θ§gnΘ®xΘ©Γζ+ΓόΘΜ
Β±xΓζ+Γό ±Θ§Θ®Ω…»Γx=eΘ§e2Θ§e3Θ§Γ≠Χε―ιΘ©Θ§gnΘ®xΘ©Γζ+ΓόΘ°
Β±nΓί3 ±Θ§gn(
)=n(1-lnn)-1ΘΦ0Θ§Κ· ΐgnΘ®xΘ©”–ΝΫΗωΝψΒψΘΜ
Β±n=2 ±Θ§gn(
)=-2ln2+1ΘΦ0Θ§Κ· ΐgnΘ®xΘ©”–ΝΫΗωΝψΒψΘΜ
Β±n=1 ±Θ§gn(
)=0Θ§Κ· ΐgnΘ®xΘ©÷Μ”–“ΜΗωΝψΒψΘΜ
Ήέ…œΥυ ωΘ§¥φ‘Ύn=1 ΙΒΟΚ· ΐgnΘ®xΘ©”–«“÷Μ”–“ΜΗωΝψΒψΘ°
Θ®ΔσΘ©fnΓδ(x)=n•xn-1Θ§
ΓΏ
=
Θ§Γύ
=
Θ°
ΫβΒΟx0=
Θ§
‘ρx0-m=
Θ§
Β±mΘΨ1 ±Θ§Θ®n+1Θ©Θ®mn-1Θ©ΘΨ0Θ§…ηhΘ®xΘ©=-xn+1+xΘ®n+1Θ©-nΘ®xΓί1Θ©Θ§
‘ρhΓδΘ®xΘ©=-Θ®n+1Θ©xn+n+1=-Θ®n+1Θ©Θ®xn-1Θ©Γή0Θ®Β±«“ΫωΒ±x=1 ±»ΓΒ»Κ≈Θ©Θ§
Υυ“‘hΘ®xΘ©‘Ύ[1Θ§+ΓόΘ©…œ «ΦθΚ· ΐΘ§
”÷“ρΈΣmΘΨ1Θ§Υυ“‘hΘ®mΘ©ΘΦhΘ®1Θ©=0Θ§Υυ“‘x0-mΘΦ0Θ§Υυ“‘x0ΘΦmΘ°
Β±0ΘΦmΘΦ1 ±Θ§Θ®n+1Θ©Θ®mn-1Θ©ΘΦ0Θ§…ηhΘ®xΘ©=-xn+1+xΘ®n+1Θ©-nΘ®0ΘΦxΓή1Θ©Θ§
‘ρhΓδΘ®xΘ©=-Θ®n+1Θ©xn+n+1=-Θ®n+1Θ©Θ®xn-1Θ©Γί0Θ®Β±«“ΫωΒ±x=1 ±»ΓΒ»Κ≈Θ©Θ§
Υυ“‘hΘ®xΘ©‘ΎΘ®0Θ§1]…œ «‘ωΚ· ΐΘ§”÷“ρΈΣ0ΘΦmΘΦ1Θ§Υυ“‘hΘ®mΘ©ΘΦhΘ®1Θ©=0Θ§Υυ“‘x0-mΘΨ0Θ§
Υυ“‘x0ΘΨmΘ°
Ήέ…œΥυ ωΘ§Β±mΘΨ1Θ§x0ΘΦmΘ°Β±0ΘΦmΘΦ1 ±Θ§x0ΘΨmΘ°
Θ®ΔρΘ©gn(x)=xn-n2lnx-1Θ§gnΓδ(x)=n•xn-1-
| n2 |
| x |
| n(xn-n) |
| x |
ΓΏxΘΨ0Θ§ΝνgnΓδ(x)=0Θ§ΒΟx=
| n | n |
Β±xΘΨ
| n | n |
Β±0ΘΦxΘΦ
| n | n |
Υυ“‘Β±x=
| n | n |
| n | n |
Β±xΓζ0 ±Θ§gnΘ®xΘ©Γζ+ΓόΘΜ
Β±xΓζ+Γό ±Θ§Θ®Ω…»Γx=eΘ§e2Θ§e3Θ§Γ≠Χε―ιΘ©Θ§gnΘ®xΘ©Γζ+ΓόΘ°
Β±nΓί3 ±Θ§gn(
| n | n |
Β±n=2 ±Θ§gn(
| n | n |
Β±n=1 ±Θ§gn(
| n | n |
Ήέ…œΥυ ωΘ§¥φ‘Ύn=1 ΙΒΟΚ· ΐgnΘ®xΘ©”–«“÷Μ”–“ΜΗωΝψΒψΘ°
Θ®ΔσΘ©fnΓδ(x)=n•xn-1Θ§
ΓΏ
| fnΓδ(x0) |
| fn-1Γδ(x0) |
| fn(m) |
| fn-1(m) |
| nx0n-1 |
| (n+1)x0n |
| mn-1 |
| mn+1-1 |
ΫβΒΟx0=
| n(mn+1-1) |
| (n+1)(mn-1) |
‘ρx0-m=
| -mn+1+m(n+1)-n |
| (n+1)(mn-1) |
Β±mΘΨ1 ±Θ§Θ®n+1Θ©Θ®mn-1Θ©ΘΨ0Θ§…ηhΘ®xΘ©=-xn+1+xΘ®n+1Θ©-nΘ®xΓί1Θ©Θ§
‘ρhΓδΘ®xΘ©=-Θ®n+1Θ©xn+n+1=-Θ®n+1Θ©Θ®xn-1Θ©Γή0Θ®Β±«“ΫωΒ±x=1 ±»ΓΒ»Κ≈Θ©Θ§
Υυ“‘hΘ®xΘ©‘Ύ[1Θ§+ΓόΘ©…œ «ΦθΚ· ΐΘ§
”÷“ρΈΣmΘΨ1Θ§Υυ“‘hΘ®mΘ©ΘΦhΘ®1Θ©=0Θ§Υυ“‘x0-mΘΦ0Θ§Υυ“‘x0ΘΦmΘ°
Β±0ΘΦmΘΦ1 ±Θ§Θ®n+1Θ©Θ®mn-1Θ©ΘΦ0Θ§…ηhΘ®xΘ©=-xn+1+xΘ®n+1Θ©-nΘ®0ΘΦxΓή1Θ©Θ§
‘ρhΓδΘ®xΘ©=-Θ®n+1Θ©xn+n+1=-Θ®n+1Θ©Θ®xn-1Θ©Γί0Θ®Β±«“ΫωΒ±x=1 ±»ΓΒ»Κ≈Θ©Θ§
Υυ“‘hΘ®xΘ©‘ΎΘ®0Θ§1]…œ «‘ωΚ· ΐΘ§”÷“ρΈΣ0ΘΦmΘΦ1Θ§Υυ“‘hΘ®mΘ©ΘΦhΘ®1Θ©=0Θ§Υυ“‘x0-mΘΨ0Θ§
Υυ“‘x0ΘΨmΘ°
Ήέ…œΥυ ωΘ§Β±mΘΨ1Θ§x0ΘΦmΘ°Β±0ΘΦmΘΦ1 ±Θ§x0ΘΨmΘ°
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΝΥΒΦ ΐ‘ΎΉν¥σ÷ΒΉν–Γ÷Β÷–ΒΡ”Π”ΟΘ§ΩΦ≤ιΝΥΖ÷άύΧ÷¬έΒΡ ΐ―ßΥΦœκΖΫΖ®Θ§―ΒΝΖΝΥΙΙ‘λΚ· ΐΖ®Ϋχ––≤ΜΒ» ΫΒΡ¥σ–Γ±»ΫœΘ§ «”–“ΜΕ®Ρ―Ε»ΧβΡΩΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 Θ§«“¬ζΉψ
Θ§«“¬ζΉψ
 Θ§aΘ§x1Θ§x2ΈΣ≥Θ ΐ,x1ΓΌx2Θ°
Θ§aΘ§x1Θ§x2ΈΣ≥Θ ΐ,x1ΓΌx2Θ°
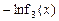 Θ§xΓ Θ®0Θ§e]Θ§»τF(x)ΒΡΉν–Γ÷ΒΈΣ6Θ§«σ Β ΐbΒΡ÷ΒΘΜ
Θ§xΓ Θ®0Θ§e]Θ§»τF(x)ΒΡΉν–Γ÷ΒΈΣ6Θ§«σ Β ΐbΒΡ÷ΒΘΜ Θ§A(x1Θ§y1)Θ§B(x2Θ§y2)(x1<x2) «Κ· ΐg(x)ΆΦœσ…œΝΫΒψΘ§»τ
Θ§A(x1Θ§y1)Θ§B(x2Θ§y2)(x1<x2) «Κ· ΐg(x)ΆΦœσ…œΝΫΒψΘ§»τ Θ§ ‘≈–Εœx0Θ§x1Θ§x2ΒΡ¥σ–ΓΘ§≤ΔΦ”“‘÷ΛΟςΘ°
Θ§ ‘≈–Εœx0Θ§x1Θ§x2ΒΡ¥σ–ΓΘ§≤ΔΦ”“‘÷ΛΟςΘ°