题目内容
已知A、B、C三点共线,O为直线外任意一点,且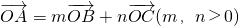 ,则
,则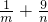 的最小值为
的最小值为
- A.8
- B.12
- C.16
- D.32
C
分析:先由A、B、C三点共线,O为直线外任意一点,且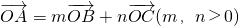 ,可知m+n=1,再利用基本不等式可求.
,可知m+n=1,再利用基本不等式可求.
解答:由题意,∵A、B、C三点共线
∴m+n=1
∴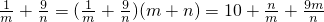 ≥16
≥16
即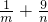 的最小值为16
的最小值为16
故选C.
点评:本题以向量为载体,考查三点共线,考查基本不等式的运用,关键是利用三点共线的条件.
分析:先由A、B、C三点共线,O为直线外任意一点,且
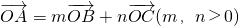 ,可知m+n=1,再利用基本不等式可求.
,可知m+n=1,再利用基本不等式可求.解答:由题意,∵A、B、C三点共线
∴m+n=1
∴
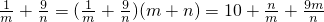 ≥16
≥16即
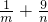 的最小值为16
的最小值为16故选C.
点评:本题以向量为载体,考查三点共线,考查基本不等式的运用,关键是利用三点共线的条件.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知A、B、C三点共线,A分
的比为λ=-
,A,B的纵坐标分别为2,5,则点C的纵坐标为( )
| BC |
| 3 |
| 8 |
| A、-10 | B、6 | C、8 | D、10 |
已知A,B,C三点共线,且A(3,-6),B(-5,2)若C点横坐标为6,则C点的纵坐标为( )
| A、-13 | B、9 | C、-9 | D、13 |