题目内容
已知向量a=(cosx,sinx),b=( ,
, ),a•b=
),a•b= ,且
,且 <x<
<x< ,则cos(x+
,则cos(x+ )的值为
)的值为
- A.

- B.

- C.-

- D.-

D
分析:由 、
、 的坐标,得
的坐标,得 •
• =
= (cosx+sinx)=
(cosx+sinx)= ,解出cosx+sinx=
,解出cosx+sinx= .由同角三角函数的关系,得(cosx-sinx)2=
.由同角三角函数的关系,得(cosx-sinx)2=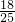 ,结合
,结合 <x<
<x< 知cosx-sinx为负数,得cosx-sinx=-
知cosx-sinx为负数,得cosx-sinx=-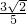 ,最后根据两角和的余弦公式,可得cos(x+
,最后根据两角和的余弦公式,可得cos(x+ )的值.
)的值.
解答:∵ =(cosx,sinx),
=(cosx,sinx), =(
=( ,
, ),
),
∴ •
• =
= cosx+
cosx+ sinx=
sinx= ,得cosx+sinx=
,得cosx+sinx=
∴(cosx-sinx)2=2-(cosx+sinx)2=2-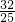 =
=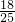
∵ <x<
<x< ,
,
∴cosx<sinx,得cosx-sinx=- =-
=-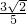
因此,cos(x+ )=cosxcos
)=cosxcos -sinxsin
-sinxsin =
= (cosx-sinx)=-
(cosx-sinx)=-
故选D
点评:本题给出向量的坐标形式,在已知数量积的情况下求三角函数的值,着重考查了两角和与差的三角函数公式和平面向量积的坐标运算等知识,属于基础题.
分析:由
 、
、 的坐标,得
的坐标,得 •
• =
= (cosx+sinx)=
(cosx+sinx)= ,解出cosx+sinx=
,解出cosx+sinx= .由同角三角函数的关系,得(cosx-sinx)2=
.由同角三角函数的关系,得(cosx-sinx)2=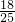 ,结合
,结合 <x<
<x< 知cosx-sinx为负数,得cosx-sinx=-
知cosx-sinx为负数,得cosx-sinx=-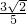 ,最后根据两角和的余弦公式,可得cos(x+
,最后根据两角和的余弦公式,可得cos(x+ )的值.
)的值.解答:∵
 =(cosx,sinx),
=(cosx,sinx), =(
=( ,
, ),
),∴
 •
• =
= cosx+
cosx+ sinx=
sinx= ,得cosx+sinx=
,得cosx+sinx=
∴(cosx-sinx)2=2-(cosx+sinx)2=2-
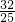 =
=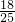
∵
 <x<
<x< ,
,∴cosx<sinx,得cosx-sinx=-
 =-
=-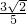
因此,cos(x+
 )=cosxcos
)=cosxcos -sinxsin
-sinxsin =
= (cosx-sinx)=-
(cosx-sinx)=-
故选D
点评:本题给出向量的坐标形式,在已知数量积的情况下求三角函数的值,着重考查了两角和与差的三角函数公式和平面向量积的坐标运算等知识,属于基础题.

练习册系列答案
相关题目