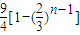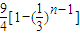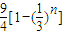题目内容
一系列椭圆都以一定直线l为准线,所有椭圆的中心都在定点M,且点M到l的距离为2,若这一系列椭圆的离心率组成以 为首项,
为首项, 为公比的等比数列,而椭圆相应的长半轴长为ai(i=1,2,…,n),则a1+a2+…+an=
为公比的等比数列,而椭圆相应的长半轴长为ai(i=1,2,…,n),则a1+a2+…+an=
- A.
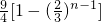
- B.
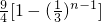
- C.
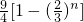
- D.
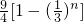
D
分析:根据椭圆的离心率组成以 为首项,
为首项, 为公比的等比数列,得出
为公比的等比数列,得出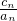 =
= •(
•( )n-1,又点M到l的距离为2,得到
)n-1,又点M到l的距离为2,得到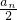 =
=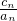 =
= •(
•( )n-1,最后利用等比数列的求和公式求和即得.
)n-1,最后利用等比数列的求和公式求和即得.
解答:∵椭圆的离心率组成以 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,
∴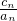 =
= •(
•( )n-1,
)n-1,
又点M到l的距离为2,
∴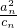 =2,
=2,
∴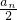 =
=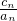 ,
,
∴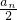 =
= •(
•( )n-1,
)n-1,
∴a1+a2+…+an=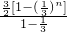 =
=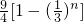 .
.
故选D.
点评:本小题主要考查椭圆的几何性质、等比数列的应用、椭圆的应用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
分析:根据椭圆的离心率组成以
 为首项,
为首项, 为公比的等比数列,得出
为公比的等比数列,得出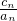 =
= •(
•( )n-1,又点M到l的距离为2,得到
)n-1,又点M到l的距离为2,得到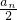 =
=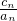 =
= •(
•( )n-1,最后利用等比数列的求和公式求和即得.
)n-1,最后利用等比数列的求和公式求和即得.解答:∵椭圆的离心率组成以
 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,∴
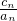 =
= •(
•( )n-1,
)n-1,又点M到l的距离为2,
∴
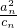 =2,
=2,∴
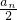 =
=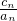 ,
,∴
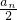 =
= •(
•( )n-1,
)n-1,∴a1+a2+…+an=
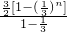 =
=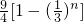 .
.故选D.
点评:本小题主要考查椭圆的几何性质、等比数列的应用、椭圆的应用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
 为首项,
为首项, 为公比的等比数列,而椭圆相应的长半轴长为ai(i=1,2,…,n),则a1+a2+…+an=( )
为公比的等比数列,而椭圆相应的长半轴长为ai(i=1,2,…,n),则a1+a2+…+an=( )