题目内容
(本小题满分12分)已知集合A={x|mx2-2x+3=0,m∈R,x∈R }.
(1)若A是空集,求m的取值范围;
(2)若A中只有一个元素,求m的值;
(3)若A中至多只有一个元素,求m的取值范围.
(1)若A是空集,求m的取值范围;
(2)若A中只有一个元素,求m的值;
(3)若A中至多只有一个元素,求m的取值范围.
(1)m>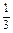
(2)m=0或m=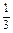
(3)m=0或m≥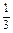 .
.
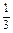
(2)m=0或m=
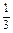
(3)m=0或m≥
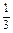 .
.解 集合A是方程mx2-2x+3=0在实数范围内的解集.
(1)∵A是空集,∴方程mx2-2x+3=0无解.∴Δ=4-12m<0,即m>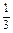 .--------4分
.--------4分
(2)∵A中只有一个元素,∴方程mx2-2x+3=0只有一个解.
若m=0,方程为-2x+3=0,只有一解x=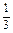 ;---------------------6分
;---------------------6分
若m≠0,则Δ=0,即4-12m=0,m=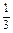 .∴m=0或m=
.∴m=0或m=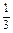 .--------------------8分
.--------------------8分
(3)A中至多只有一个元素包含A中只有一个元素和A是空集两种含义,根据(1)、(2)的结果,得m=0或m≥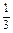 . -------------------------------12分
. -------------------------------12分
(1)∵A是空集,∴方程mx2-2x+3=0无解.∴Δ=4-12m<0,即m>
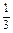 .--------4分
.--------4分(2)∵A中只有一个元素,∴方程mx2-2x+3=0只有一个解.
若m=0,方程为-2x+3=0,只有一解x=
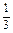 ;---------------------6分
;---------------------6分若m≠0,则Δ=0,即4-12m=0,m=
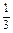 .∴m=0或m=
.∴m=0或m=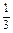 .--------------------8分
.--------------------8分(3)A中至多只有一个元素包含A中只有一个元素和A是空集两种含义,根据(1)、(2)的结果,得m=0或m≥
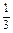 . -------------------------------12分
. -------------------------------12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
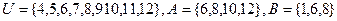
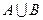 和
和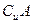 ; (2)写出集合
; (2)写出集合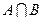 的所有子集。
的所有子集。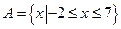 ,
,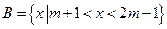 且
且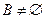 ,若
,若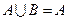 ,则( )
,则( )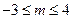
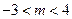
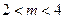
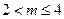
 ,
,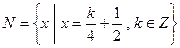 ,则( ).
,则( ).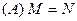
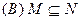
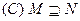
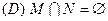
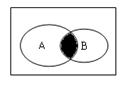
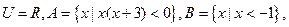 则图中阴影部分表示的集合为 ( )
则图中阴影部分表示的集合为 ( )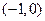 B
B 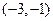
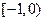 D
D 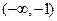
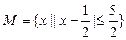 ,
,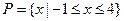 ,则
,则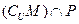 等( )
等( )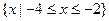
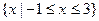
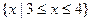
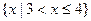
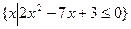 B=
B=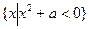
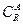 )∩B=B,求实数a的取值范围。
)∩B=B,求实数a的取值范围。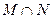 为( )
为( )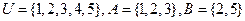 ,则
,则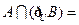 ( )
( )