题目内容
(本小题满分14分)
已知函数 .
.
(Ⅰ)若函数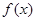 在定义域内为增函数,求实数
在定义域内为增函数,求实数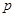 的取值范围;
的取值范围;
(Ⅱ)当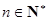 时,试判断
时,试判断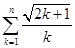 与
与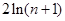 的大小关系,并证明你的结论;
的大小关系,并证明你的结论;
(Ⅲ)
当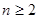 且
且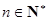 时,证明:
时,证明: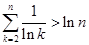 .
.
【答案】
(Ⅰ)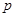 的取值范围为
的取值范围为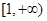 .(Ⅱ)当
.(Ⅱ)当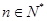 时,
时,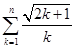
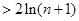 .
.
(Ⅲ)见解析.
【解析】(I)求函数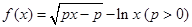 .的导数,注意定义域,令导函数大于或等于0,分离参数
.的导数,注意定义域,令导函数大于或等于0,分离参数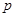 ,令一端配方求出最值即得
,令一端配方求出最值即得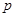 的范围;(II)由(Ⅰ)可知:
的范围;(II)由(Ⅰ)可知: 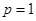 时,
时,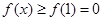 ,
,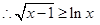 (当
(当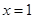 时,等号成立),令
时,等号成立),令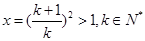 ,则
,则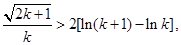 取
取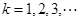 两边分别相加整理即得结论;(III)由(2)知,当
两边分别相加整理即得结论;(III)由(2)知,当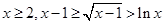 ,令
,令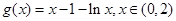 求导可得最小值
求导可得最小值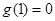 ,所以
,所以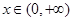 时,
时,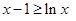 (当且仅当
(当且仅当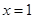 时,等号成立),令
时,等号成立),令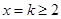 ,则
,则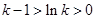 ,所以
,所以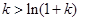 ,
,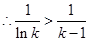 ,因而可得
,因而可得 ,所以
,所以 , 所以
, 所以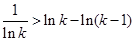 ,然后不等式累加证明即可.
,然后不等式累加证明即可.
(Ⅰ) ,函数
,函数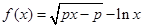 的定义域为
的定义域为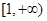 .
.
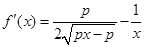 .
.
依题意,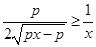 在
在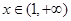 恒成立,
恒成立,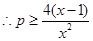 在
在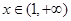 恒成立.
恒成立.
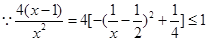 ,
,
 ,∴
,∴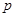 的取值范围为
的取值范围为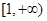 .
……………………………………………………… (4分)
.
……………………………………………………… (4分)
(Ⅱ)当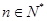 时,
时,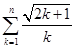
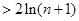 .
.
证明:当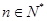 时,欲证
时,欲证
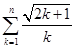
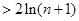 ,只需证
,只需证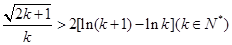 .
.
由(Ⅰ)可知:取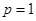 ,则
,则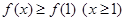 ,
,
而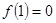 ,
,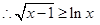 (当
(当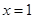 时,等号成立).
时,等号成立).
用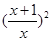 代换
代换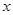 ,得
,得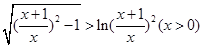 ,即
,即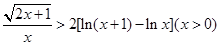 ,
,
∴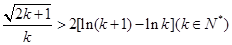 .
.
在上式中分别取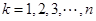 ,并将同向不等式相加,得
,并将同向不等式相加,得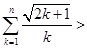
 .
.
∴当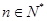 时,
时,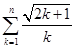
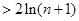 .
………………………………………… (9分)
.
………………………………………… (9分)
(Ⅲ)由(Ⅱ)可知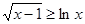 (
(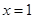 时,等号成立).
时,等号成立).
而当 时:
时: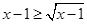 ,∴ 当
,∴ 当 时,
时, .
.
设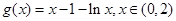 ,则
,则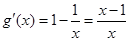 ,
,
∴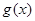 在
在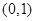 上递减,在
上递减,在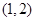 上递增,
上递增,
∴ ,即
,即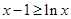 在
在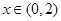 时恒成立.
时恒成立.
故当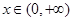 时,
时,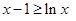 (当且仅当
(当且仅当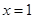 时,等号成立).
…… ①
时,等号成立).
…… ①
用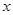 代换
代换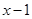 得:
得:
 (当且仅当
(当且仅当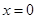 时,等号成立).
…… ②
时,等号成立).
…… ②
当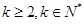 时,由①得
时,由①得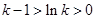 ,
,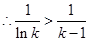 .
.
当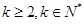 时,由②得
时,由②得
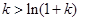 ,用
,用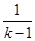 代换
代换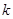 ,得
,得 .
.
∴当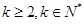 时,
时, ,即
,即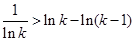 .
.
在上式中分别取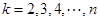 ,并将同向不等式相加,得
,并将同向不等式相加,得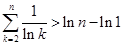 .
.
故当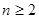 且
且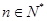 时,
时, .
…………………………………………………(14分)
.
…………………………………………………(14分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)