题目内容
已知m,n是方程lg2x+lg15lgx+lg3lg5=0的两根,则mn=
- A.-(lg3+lg5)
- B.lg3lg5
- C.

- D.

D
分析:由已知m,n是方程lg2x+lg15lgx+lg3lg5=0的两根,结合韦达定理(根与系数的关系),我们易得到lgm+lgn=-lg15,根据对数的运算性质易得到结论.
解答:令t=lgx,则原方程可化为
t2+lg15t+lg3lg5=0
∵m,n是方程lg2x+lg15lgx+lg3lg5=0的两根
∴lg和lgn是方程t2+lg15t+lg3lg5=0的两根
由韦达定理得:lgm+lgn=-lg15
即lgmn=lg
∴mn=
故选D
点评:本题考查的知识点是一元二次方程的根的分布与系数的关系,结合韦达定理得到lgm+lgn=-lg15是解答本题的关键.
分析:由已知m,n是方程lg2x+lg15lgx+lg3lg5=0的两根,结合韦达定理(根与系数的关系),我们易得到lgm+lgn=-lg15,根据对数的运算性质易得到结论.
解答:令t=lgx,则原方程可化为
t2+lg15t+lg3lg5=0
∵m,n是方程lg2x+lg15lgx+lg3lg5=0的两根
∴lg和lgn是方程t2+lg15t+lg3lg5=0的两根
由韦达定理得:lgm+lgn=-lg15
即lgmn=lg

∴mn=

故选D
点评:本题考查的知识点是一元二次方程的根的分布与系数的关系,结合韦达定理得到lgm+lgn=-lg15是解答本题的关键.

练习册系列答案
相关题目
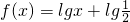 的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;
的图象与函数g(x)=lg(-x)+2的图象关于直线l对称; 的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;
的图象与函数g(x)=lg(-x)+2的图象关于直线l对称; 的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;
的图象与函数g(x)=lg(-x)+2的图象关于直线l对称;