题目内容
(本小题12分)已知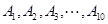 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为
等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为 .
.
(Ⅰ)如果该同学10所高校的考试都参加,试求恰有2所通过的概率;
(Ⅱ)假设该同学参加每所高校考试所需的费用均为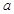 元,该同学决定按
元,该同学决定按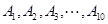 顺序参加考试,一旦通过某所高校的考试,就不再参加其它高校的考试,试求该同学参加考试所需费用
顺序参加考试,一旦通过某所高校的考试,就不再参加其它高校的考试,试求该同学参加考试所需费用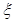 的分布列及数学期望.
的分布列及数学期望.
【答案】
(1)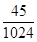 (2)
(2)
【解析】
试题分析:.解(Ⅰ)因为该同学通过各校考试的概率均为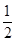 ,所以该同学恰好通过2所高校自主招生考试的概率为
,所以该同学恰好通过2所高校自主招生考试的概率为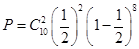
 . ………………4分
. ………………4分
(Ⅱ)设该同学共参加了 次考试的概率为
次考试的概率为 (
( ).
).
∵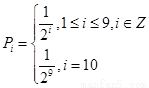 , ……………………6分
, ……………………6分
∴所以该同学参加考试所需费用 的分布列如下:
的分布列如下:
|
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
………………………………………………8分
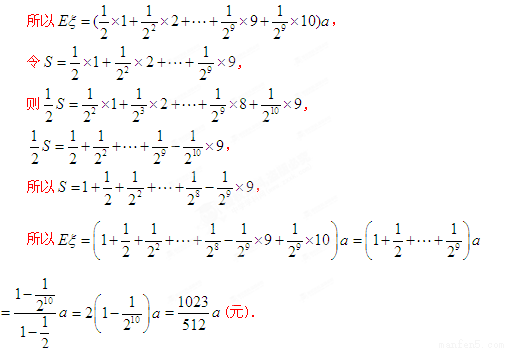
………………………………………………12分
考点:本试题考查了分布列和二项分布的概率计算。
点评:解决分布列的求解关键是弄清楚各个取值的概率值,同时要熟练的结合二项分布来求解概率值和分布列,从而求解期望值,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

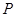


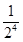
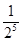
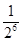
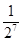
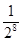
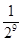
 中,
中, 。
。 中,
中, ,求数列
,求数列 项和
项和 .
. 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程 ;
; 过
过 且与圆C相切,求直线
且与圆C相切,求直线 ,使直线
,使直线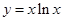
 处的切线方程。
处的切线方程。