Question

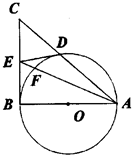
选修4-1；几何证明选讲．
如图，在△ABC中，∠B=90°，以AB为直径的⊙O交AC于D，点E为BC的中点，连接DE、AE，AE交⊙O于点F．
（1）求证：DE是⊙O的切线；（2）若⊙O的直径为2，求AD•AC的值．

Answer 1

分析：（1）要证明DE是⊙O的切线，只需要证明 EDO=90°，而已知∠B=90°，所以问题转化为证明EDO=∠EBO=90°，根据已知可通过证明△ODE≌△OBE即可
（2）由已知容易证明△ABD∽△ACB，从而可得

AB

AC

=

AD

AB

，即AB²=AD•AC，可

解答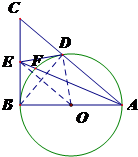：证明：（1）连接OD，OE
∵AO=OB，CE=EB∴OE∥AC，OE=

1

2

AC
∴∠CAB=∠EOB，∠ADO=∠DOE
∵OA=OD
∴∠CAB=∠ADO
则∠DOE=∠EOB
EDO=∠EBO=90°又∵OD=OB，OE是公共边．
∴△ODE≌△OBE
∴EDO=∠EBO=90°
∴DE是⊙O的切线                           …（5分）
（2）连接BD，显然BD是Rt△ABC斜边上的高．
可得△ABD∽△ACB所以

AB

AC

=

AD

AB

，即AB²=AD•AC
所以AD•AC=4                           …（10分）

点评：本题主要考查了切线的证明：常有两种辅助线的添加：①有半径，常要证明垂直②有过一点与已知直线垂直的直线，需要证明该直线是半径．