题目内容

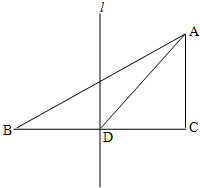如图，在△ABC中，|
AB
|=3，|
AC
|=1，l为BC的垂直平分线，l与BC交于点D，F为线段AD上的任意一点，且AC⊥BC，则
AF
•(
FB
+
FC
)的最大值为
3
2
3
2
．
分析：首先利用D为线段BC中点，证明出
FB
+
FC
=2
FD
，从而
AF
•(
FB
+
FC
)可以化简为2|
AF
|•|
FD
|=2|
AF
|（|
AD
|-|
AF
|），然后利用直角三角形的勾股定理计算出|
AD
|=
3
，代入化简的式子，最后利用基本不等式可以求得
AF
•(
FB
+
FC
)的最大值．
解答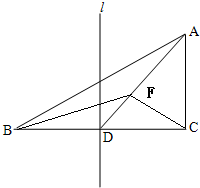：解：∵D为线段BC中点
∴
DB
+
DC
=
O
⇒(
FB
-
FD
)+(
FC
-
FD
)=
O

∴
FB
+
FC
=2
FD

∴
AF
•(
FB
+
FC
)=
AF
• 2
FD
=2|
AF
|•|
FD
| cos0°
=2|
AF
|•|
FD
|=2|
AF
|（|
AD
|-|
AF
|）
∵Rt△ABC中，|
AB
|=3，|
AC
|=1，
∴|
BC
| =
32-12
=2
2

可得Rt△ADC中，|
CD
| =
1
2
|
BC
| =
2

∴|
AD
| =
(
2
)2+12
=
3

所以
AF
•(
FB
+
FC
)=2|
AF
|（
3
-|
AF
|）
∵0＜|
AF
|＜
3

∴
|AF|
(
3
-
|AF|
)
≤
|AF|
+(
3
-
|AF|
)
2
=
3
2
⇒|
AF
|（
3
-|
AF
|）≤
3
4

所以当且仅|
AF
|=
3
2
时，
AF
•(
FB
+
FC
)的最大值为
3
2
点评：本题以直角三角形中的中线为载体，考查了向量在平面几何中的应用，属于中档题．请同学们注意在解题的过程中用到了基本不等式求最值，要交待等号成立的条件．
练习册系列答案
相关题目
精英家教网如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
AD=4cm．
（1）求：⊙O的直径BE的长；
（2）计算：△ABC的面积．
精英家教网如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=
3
BD，BC=2BD，则sinC的值为（　　）
A、
3
3
B、
3
6
C、
6
3
D、
6
6
如图，在△ABC中，设
AB
=a，
AC
=b，AP的中点为Q，BQ的中点为R，CR的中点恰为P．
（Ⅰ）若
AP
=λa+μb，求λ和μ的值；
（Ⅱ）以AB，AC为邻边，AP为对角线，作平行四边形ANPM，求平行四边形ANPM和三角形ABC的面积之比
S平行四边形ANPM
S△ABC
．
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
（1）求∠ADC的大小；
（2）求AB的长．
如图，在△ABC中，已知
BD
=2
DC
，则
AD
=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网