题目内容
已知函数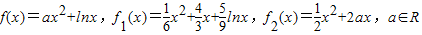
(1)求证:函数f(x)在点(e,f(e))处的切线横过定点,并求出定点的坐标;
(2)若f(x)<f2(x)在区间(1,+∞)上恒成立,求a的取值范围;
(3)当
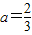 时,求证:在区间(1,+∞)上,满足f1(x)<g(x)<f2(x)恒成立的函数g(x)有无穷多个.
时,求证:在区间(1,+∞)上,满足f1(x)<g(x)<f2(x)恒成立的函数g(x)有无穷多个.
【答案】分析:(1)先求出导数 ,根据导数的几何意义得出f(x)在点(e,f(e))处的切线的斜率为
,根据导数的几何意义得出f(x)在点(e,f(e))处的切线的斜率为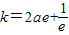 ,从而写出切线方程得出切线恒过定点;
,从而写出切线方程得出切线恒过定点;
(2)先令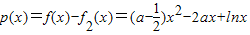 <0,对x∈(1,+∞)恒成立,
<0,对x∈(1,+∞)恒成立,
利用导数求出p(x)在区间(1,+∞)上是减函数,从而得出:要使p(x)<0在此区间上恒成立,只须满足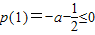 ,由此解得a的范围即可.
,由此解得a的范围即可.
(3)当 时,
时,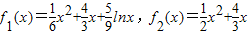 .
.
记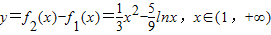 .利用导数研究它的单调性,得出y=f2(x)-f1(x)在(1,+∞)上为增函数,最后得到满足f1(x)<g(x)<f2(x)恒成立的函数g(x)有无穷多个.
.利用导数研究它的单调性,得出y=f2(x)-f1(x)在(1,+∞)上为增函数,最后得到满足f1(x)<g(x)<f2(x)恒成立的函数g(x)有无穷多个.
解答:解:(1)因为 ,所以f(x)在点(e,f(e))处的切线的斜率为
,所以f(x)在点(e,f(e))处的切线的斜率为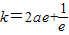 ,
,
所以f(x)在点(e,f(e))处的切线方程为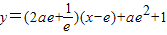 ,
,
整理得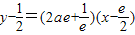 ,所以切线恒过定点
,所以切线恒过定点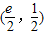 .
.
(2)令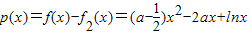 <0,对x∈(1,+∞)恒成立,
<0,对x∈(1,+∞)恒成立,
因为 (*)
(*)
令p'(x)=0,得极值点x1=1,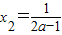 ,
,
①当 时,有x2>x1=1,即
时,有x2>x1=1,即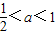 时,在(x2,+∞)上有p'(x)>0,
时,在(x2,+∞)上有p'(x)>0,
此时p(x)在区间(x2,+∞)上是增函数,并且在该区间上有p(x)∈(p(x2),+∞),不合题意;
②当a≥1时,有x2<x1=1,同理可知,p(x)在区间(1,+∞)上,有p(x)∈(p(1),+∞),也不合题意;
③当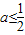 时,有2a-1≤0,此时在区间(1,+∞)上恒有p'(x)<0,
时,有2a-1≤0,此时在区间(1,+∞)上恒有p'(x)<0,
从而p(x)在区间(1,+∞)上是减函数;
要使p(x)<0在此区间上恒成立,只须满足
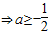 ,
,
所以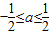 .
.
综上可知a的范围是 .
.
(3)当 时,
时,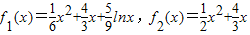
记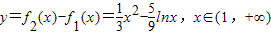 .
.
因为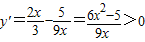 ,所以y=f2(x)-f1(x)在(1,+∞)上为增函数,
,所以y=f2(x)-f1(x)在(1,+∞)上为增函数,
所以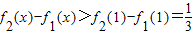 ,设
,设 ,则f1(x)<R(x)<f2(x),
,则f1(x)<R(x)<f2(x),
所以在区间(1,+∞)上,满足f1(x)<g(x)<f2(x)恒成立的函数g(x)有无穷多个.
点评:本题主要考查利用导数研究曲线上某点切线方程、导函数的正负与原函数的单调性之间的关系等,注意应用导数的性质:当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.
 ,根据导数的几何意义得出f(x)在点(e,f(e))处的切线的斜率为
,根据导数的几何意义得出f(x)在点(e,f(e))处的切线的斜率为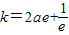 ,从而写出切线方程得出切线恒过定点;
,从而写出切线方程得出切线恒过定点;(2)先令
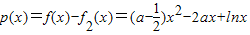 <0,对x∈(1,+∞)恒成立,
<0,对x∈(1,+∞)恒成立,利用导数求出p(x)在区间(1,+∞)上是减函数,从而得出:要使p(x)<0在此区间上恒成立,只须满足
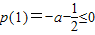 ,由此解得a的范围即可.
,由此解得a的范围即可.(3)当
 时,
时,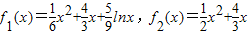 .
.记
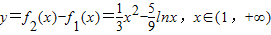 .利用导数研究它的单调性,得出y=f2(x)-f1(x)在(1,+∞)上为增函数,最后得到满足f1(x)<g(x)<f2(x)恒成立的函数g(x)有无穷多个.
.利用导数研究它的单调性,得出y=f2(x)-f1(x)在(1,+∞)上为增函数,最后得到满足f1(x)<g(x)<f2(x)恒成立的函数g(x)有无穷多个.解答:解:(1)因为
 ,所以f(x)在点(e,f(e))处的切线的斜率为
,所以f(x)在点(e,f(e))处的切线的斜率为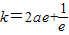 ,
,所以f(x)在点(e,f(e))处的切线方程为
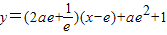 ,
,整理得
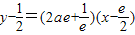 ,所以切线恒过定点
,所以切线恒过定点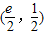 .
.(2)令
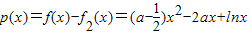 <0,对x∈(1,+∞)恒成立,
<0,对x∈(1,+∞)恒成立,因为
 (*)
(*)令p'(x)=0,得极值点x1=1,
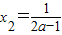 ,
,①当
 时,有x2>x1=1,即
时,有x2>x1=1,即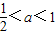 时,在(x2,+∞)上有p'(x)>0,
时,在(x2,+∞)上有p'(x)>0,此时p(x)在区间(x2,+∞)上是增函数,并且在该区间上有p(x)∈(p(x2),+∞),不合题意;
②当a≥1时,有x2<x1=1,同理可知,p(x)在区间(1,+∞)上,有p(x)∈(p(1),+∞),也不合题意;
③当
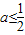 时,有2a-1≤0,此时在区间(1,+∞)上恒有p'(x)<0,
时,有2a-1≤0,此时在区间(1,+∞)上恒有p'(x)<0,从而p(x)在区间(1,+∞)上是减函数;
要使p(x)<0在此区间上恒成立,只须满足

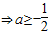 ,
,所以
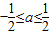 .
.综上可知a的范围是
 .
.(3)当
 时,
时,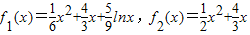
记
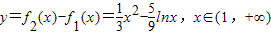 .
.因为
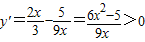 ,所以y=f2(x)-f1(x)在(1,+∞)上为增函数,
,所以y=f2(x)-f1(x)在(1,+∞)上为增函数,所以
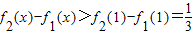 ,设
,设 ,则f1(x)<R(x)<f2(x),
,则f1(x)<R(x)<f2(x),所以在区间(1,+∞)上,满足f1(x)<g(x)<f2(x)恒成立的函数g(x)有无穷多个.
点评:本题主要考查利用导数研究曲线上某点切线方程、导函数的正负与原函数的单调性之间的关系等,注意应用导数的性质:当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
相关题目
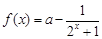 .
.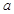 为何实数
为何实数 总是为增函数;(2)确定
总是为增函数;(2)确定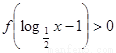
 .
.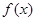 在点
在点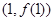 处的切线恒过定点,并求出定点坐标;
处的切线恒过定点,并求出定点坐标;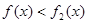 在区间
在区间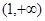 上恒成立,求
上恒成立,求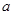 的取值范围;
的取值范围;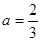 时,求证:在区间
时,求证:在区间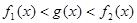 恒成立的函数
恒成立的函数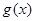
 .
. 为何实数
为何实数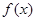 总是为增函数;
总是为增函数;