题目内容
有一道解三角形的题目,因纸张破损有一个条件模糊不清,具体如下:“在△ABC中,已知 , ,求角A.”经推断,破损处的条件为三角形一边的长度,且答案提示
, ,求角A.”经推断,破损处的条件为三角形一边的长度,且答案提示 .试在横线上将条件补充完整.
.试在横线上将条件补充完整.
【答案】分析:要把横线处补全,就要把A的度数作为已知条件求b和c的值,由a,A和B的度数,根据正弦定理求出b的长,再由三角形的内角和定理求出C的度数,由a,b及cosC,利用余弦定理即可求出c的长.
解答:解:由题意可得横线上将条件为b的值,或为c的值.
①当横线上将条件为b的值时,由正弦定理可知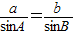 ,
,
∴b=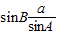 =
=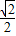 ×
×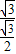 =
=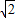 .
.
②当横线上将条件为c的值时,根据正弦定理得: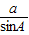 =
=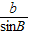 ,又a=
,又a=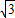 ,sinB=
,sinB=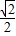 ,sinA=
,sinA=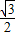 ,
,
所以,b=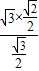 =
=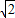 ,又C=180°-45°-60°=75°,
,又C=180°-45°-60°=75°,
所以cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°=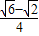 ,
,
所以c2=a2+b2-2abcosC=3+2-2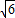 ×
×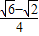 =
=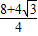 =
=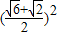 ,
,
则c=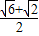 .
.
故答案为:b=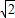 ,或
,或 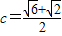 .
.
点评:此题考查学生灵活运用正弦、余弦定理化简求值,灵活运用两角和与差的余弦函数公式化简求值,是一道中档题.把A的度数看做已知条件求b或c的长度是解本题的基本思路.
解答:解:由题意可得横线上将条件为b的值,或为c的值.
①当横线上将条件为b的值时,由正弦定理可知
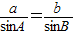 ,
,∴b=
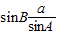 =
=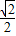 ×
×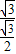 =
=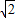 .
.②当横线上将条件为c的值时,根据正弦定理得:
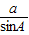 =
=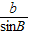 ,又a=
,又a=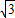 ,sinB=
,sinB=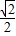 ,sinA=
,sinA=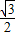 ,
,所以,b=
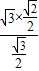 =
=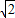 ,又C=180°-45°-60°=75°,
,又C=180°-45°-60°=75°,所以cos75°=cos(45°+30°)=cos45°cos30°-sin45°sin30°=
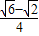 ,
,所以c2=a2+b2-2abcosC=3+2-2
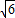 ×
×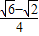 =
=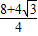 =
=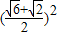 ,
,则c=
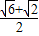 .
.故答案为:b=
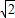 ,或
,或 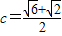 .
.点评:此题考查学生灵活运用正弦、余弦定理化简求值,灵活运用两角和与差的余弦函数公式化简求值,是一道中档题.把A的度数看做已知条件求b或c的长度是解本题的基本思路.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目