题目内容
已知x+y=1,若不等式
+
≥9对任意正实数x,y恒成立,则正实数a的最小值为
| 1 |
| x |
| a |
| y |
4
4
.分析:根据不等式
+
≥9对任意正实数x,y恒成立,可得(
+
)min≥9,利用1的代换,求出
+
最小值,即可求得结论.
| 1 |
| x |
| a |
| y |
| 1 |
| x |
| a |
| y |
| 1 |
| x |
| a |
| y |
解答:解:∵不等式
+
≥9对任意正实数x,y恒成立,
∴(
+
)min≥9
∵正实数x,y满足x+y=1,
∴
+
=(x+y)(
+
)=1+a+
+
≥1+a+2
∴1+a+2
≥9
∴1+
≥3
∴a≥4
∴正实数a的最小值为4
故答案为:4
| 1 |
| x |
| a |
| y |
∴(
| 1 |
| x |
| a |
| y |
∵正实数x,y满足x+y=1,
∴
| 1 |
| x |
| a |
| y |
| 1 |
| x |
| a |
| y |
| y |
| x |
| ax |
| y |
| a |
∴1+a+2
| a |
∴1+
| a |
∴a≥4
∴正实数a的最小值为4
故答案为:4
点评:本题考查不等式恒成立问题,解题的关键是将不等式
+
≥9对任意正实数x,y恒成立,转化为(
+
)min≥9,属于中档题.本题解法是此类题的通用解法,要好好体会
| 1 |
| x |
| a |
| y |
| 1 |
| x |
| a |
| y |

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
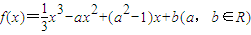
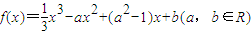

 ,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,求实数m的取值范围.
,若方程g(x)-m=0在区间[-2,2]上有两个不相等的实数根,求实数m的取值范围.