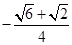题目内容
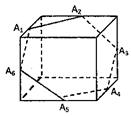
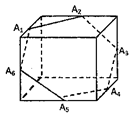
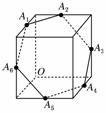
如图,圆O过正方体六条棱的中点A,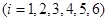 ,此圆被正方体六条棱的中点分成六段弧,记弧
,此圆被正方体六条棱的中点分成六段弧,记弧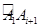 在圆O中所对的圆心角为
在圆O中所对的圆心角为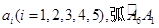 所对的圆心角为
所对的圆心角为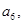 则
则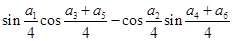 等于( )
等于( )
A.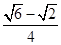 | B.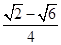 | C.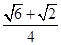 | D.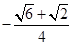 |
B
解析考点:两角和与差的正弦函数.
分析:依题意根据六段弦相等,推断6个圆心角相等即60°,代入原式,利用正弦的两角和公式得出原式等于sin15°.再利用sin(60°-45°)两角和公式得出sin15°的值,进而得出答案.
解答:解:∵如图A1A2=A2A3=A3A4=A4A5=A5A6=A6A1
∴α1=α2=α3=α4=α5=α6=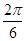 =60°
=60°
∴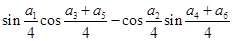
=sin cos
cos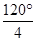 -cos
-cos sin
sin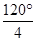
=sin( -
-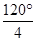 )
)
=-sin15°
又∵sin15°=sin(60°-45°)
=sin60°cos45°-cos60°sin45°
=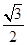 ×
× -
-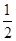 ×
×
=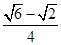
∴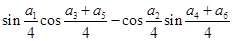 =
=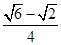
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
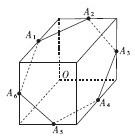 如图,圆O过正方体六条棱的中点Ai(i=1,2,3,4,5,6),此圆被正方体六条棱的中点分成六段弧,记弧AiAi+1在圆O中所对的圆心角为αi(i=1,2,3,4,5),弧A6A1所对的圆心角为α6,则sin
如图,圆O过正方体六条棱的中点Ai(i=1,2,3,4,5,6),此圆被正方体六条棱的中点分成六段弧,记弧AiAi+1在圆O中所对的圆心角为αi(i=1,2,3,4,5),弧A6A1所对的圆心角为α6,则sin| α1 |
| 4 |
| α3+α5 |
| 4 |
| α2 |
| 4 |
| α4+α6 |
| 4 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
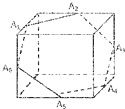 如图,圆O过正方体六条棱的中点A,此圆被正方体六条棱的中点分成六段弧,记弧
如图,圆O过正方体六条棱的中点A,此圆被正方体六条棱的中点分成六段弧,记弧
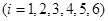 ,此圆被正方体六条棱的中点分成六段弧,记弧
,此圆被正方体六条棱的中点分成六段弧,记弧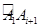 在圆O中所对的圆心角为
在圆O中所对的圆心角为 所对的圆心角为
所对的圆心角为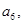 则
则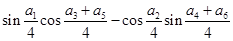 等于( )
等于( ) B.
B.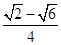 C.
C.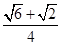 D.
D.