题目内容
直平行六面体的侧棱长是100 cm，底面相邻边长分别为23 cm和11 cm，底面的两条对角线的比是2∶3，求它的两个对角面的面积．
答案：
解析：
解析：
解析：本题关键是求出底面两条对角线的长，可以引进辅助未知数x．设两条对角线的长为2x和3x，求出x即可得对角面面积．
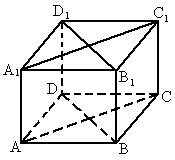
如下图所示，已知AC1是直平行六面体，所以两个对角面都是矩形，其侧棱AA1是矩形的高．
又AB＝23 cm，AD＝11 cm，AA1＝100 cm，
且BD∶AC＝2∶3，
设BD＝2x，AC＝3x，
由平行四边形对角线的性质得：BD2＋AC2＝2(AB2＋AD2)，即(2x)2＋(3x)2＝2(232＋112)．
化简得13x2＝1 300，则x＝10，
∴对角线BD＝2x＝20(cm)，AC＝3x＝30(cm)．故对角面BDD1B1的面积＝BD×BB1＝20×100＝2 000(cm2)，
对角面ACC1A1的面积＝AC×AA1＝30×100＝3 000(cm2)．
练习册系列答案
相关题目
，则它的两个对角面的面积分别为___________．
，则它的两个对角面的面积分别为___________．
