题目内容
长方体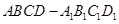 中,
中,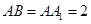 ,
,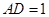 ,
,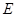 为
为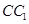 的中点,则异面直线
的中点,则异面直线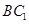 与
与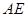 所成角的余弦值为
所成角的余弦值为
A.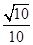 | B.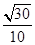 | C.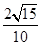 | D.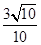 |
B
解析试题分析:建立空间直角坐标系,先相关点的坐标,再相关向量的坐标,再进行运算.解析:建立坐标系如图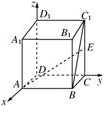
则A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2).=(-1,0,2),A=(-1,2,1),cos<BC1,AE>═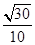
所以异面直线BC1与AE所成角的余弦值为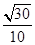 ,故选B
,故选B
考点:异面直线所成的角
点评:本题主要考查用向量法求异面直线所成的角,属于基础题。

练习册系列答案
相关题目
设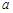 、
、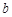 是两条不同的直线,
是两条不同的直线,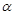 、
、 是两个不同的平面,是下列命题中正确的是( )
是两个不同的平面,是下列命题中正确的是( )
A.若 , ,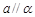 ,则 ,则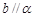 |
B.若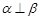 , ,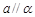 ,则 ,则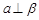 |
C.若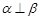 , ,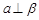 ,则 ,则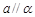 |
D.若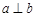 , , , , ,则 ,则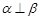 |
在三棱柱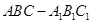 中,各侧面均为正方形,侧面
中,各侧面均为正方形,侧面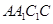 的对角线相交于点
的对角线相交于点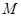 ,则
,则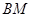 与平面
与平面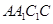 所成角的大小是( )
所成角的大小是( )
| A.30° | B.45° | C.60° | D.90 |
如图,在正方体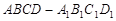 中,
中,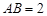 .则点
.则点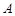 到面
到面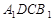 的距离是( )
的距离是( )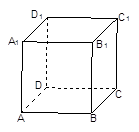
A.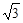 | B.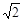 | C.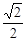 | D.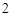 |
如图,在正方体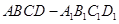 中,
中,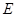 、
、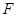 分别为棱
分别为棱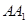 、
、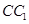 的中点,则在空间中与直线
的中点,则在空间中与直线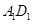 、
、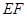 、CD都相交的直线有
、CD都相交的直线有
| A.1条 | B.2条 | C.3条 | D.无数条 |
已知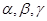 是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①
是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①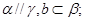 ②
②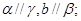 ③
③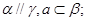 如果命题
如果命题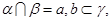 且_______,则
且_______,则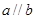 为真命题,则可以在横线处填入的条件是( )
为真命题,则可以在横线处填入的条件是( )
| A.①或② | B.②或③ | C.①或③ | D.只有② |
a,b,c表示三条不重合的直线,M表示平面,给出下列四个命题:①若a∥M,b∥M,则a∥b;②若b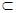 M,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有
M,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有
| A.0个 | B.1个 | C.2个 | D.3个 |
设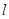 ,
,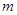 是两条不同的直线,
是两条不同的直线,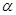 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若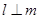 , ,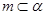 ,则 ,则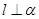 | B.若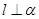 , ,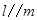 ,则 ,则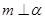 |
C.若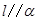 , ,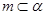 ,则 ,则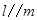 | D.若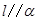 , ,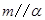 ,则 ,则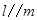 |
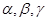 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: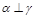 ,
,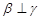 ,则
,则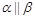 ;
;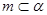 ,
,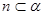 ,
,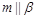 ,
,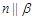 ,则
,则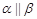 ;
;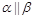 ,
,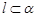 ,则
,则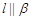 ;
;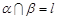 ,
,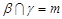 ,
,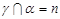 ,
,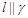 ,则
,则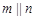 其中真命
其中真命