题目内容
(2008•南京模拟)函数f (x)是定义在[0,1]上的函数,满足f (x)=2f (
),且f (1)=1,在每一个区间(
,
](k=1,2,3,…)上,y=f (x)的图象都是斜率为同一常数m的直线的一部分,记直线x=
,x=
,x轴及函数y=f (x)的图象围成的梯形面积为an(n=1,2,3,…),则数列{an}的通项公式为
.(用最简形式表示)
| x |
| 2 |
| 1 |
| 2k |
| 1 |
| 2k-1 |
| 5 |
| 3×2n |
| 1 |
| 2n-1 |
| 12-m |
| 9×22n+1 |
| 12-m |
| 9×22n+1 |
分析:先根据f(0)=2f(0),求出f(0)及f(1)的值,归纳总结得f(
)=
,然后当
<x≤
时,f(x)=
+m(x-
)
,利用体形的面积公式可得ak=
[
+
+m(
-
)]×(
-
)=
,从而可求
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
| 1 |
| 2 |
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
,利用体形的面积公式可得ak=
| 1 |
| 2 |
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
| 5 |
| 3×2k |
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
| 5 |
| 3×2k |
| 12-m |
| 9×22k+1 |
解答:解:由f(0)=2f(0),得f(0)=0
由 f(1)=2f(
)及f(1)=1,得 f(
)=
f(1)=
同理,f(
)=
f(
)=
归纳得 f(
) =
当 x∈(
,
]时,1f(x)=
+m(x-
)
ak=
[
+
+m(
-
)]×(
-
)=
∴an=
故答案为:
由 f(1)=2f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
同理,f(
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
归纳得 f(
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
当 x∈(
| 1 |
| 2k |
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
ak=
| 1 |
| 2 |
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
| 5 |
| 3×2k |
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
| 5 |
| 3×2k |
| 12-m |
| 9×22k+1 |
∴an=
| 12-m |
| 9×22n+1 |
故答案为:
| 12-m |
| 9×22n+1 |
点评:本小题主要考查函数、数列等基本知识,考查分析问题和解决问题的能力,属于综合性试题,有一定的难度.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
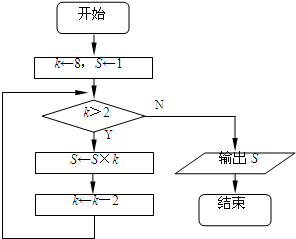 (2008•南京模拟)如图所示的流程图输出的结果是
(2008•南京模拟)如图所示的流程图输出的结果是