题目内容
(本小 题满分14分)设奇函数
题满分14分)设奇函数 对任意
对任意 都有
都有
 求
求 和
和 的值;
的值;
 数列
数列 满足:
满足: =
= +
+
 ,数列
,数列 是等差数列吗?请
是等差数列吗?请 给予证明
给予证明 ;
;
 设
设 与
与 为两个给定的不同的正整数,
为两个给定的不同的正整数, 是满足(2)中条件的数列,
是满足(2)中条件的数列,
证明:
 .
.
 题满分14分)设奇函数
题满分14分)设奇函数 对任意
对任意 都有
都有
 求
求 和
和 的值;
的值; 数列
数列 满足:
满足: =
= +
+
 ,数列
,数列 是等差数列吗?请
是等差数列吗?请 给予证明
给予证明 ;
; 设
设 与
与 为两个给定的不同的正整数,
为两个给定的不同的正整数, 是满足(2)中条件的数列,
是满足(2)中条件的数列,证明:

 .
.解:(1) ,且
,且 是奇函数
是奇函数

 ,故
,故 ……………………2分
……………………2分
因为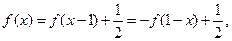 所以
所以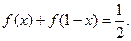
令 ,得
,得 ,即
,即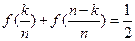 .…………
.………… …4分
…4分
(2)设
又
两式相加
 .
.
所以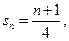 ………………6分
………………6分
故 ………………7分
………………7分
又 .故数列
.故数列 是等差数列.………………8分
是等差数列.………………8分
(3)

要证:

即 ………………10分
………………10分
∵
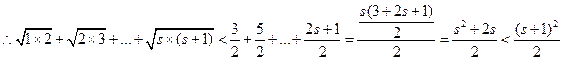 即
即 ,从而
,从而 ………………12分
………………12分
又 恒成立,
恒成立,
所以有 恒成立
恒成立
即

 …14分
…14分
 ,且
,且 是奇函数
是奇函数
 ,故
,故 ……………………2分
……………………2分因为
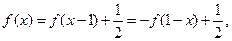 所以
所以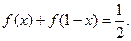
令
 ,得
,得 ,即
,即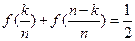 .…………
.………… …4分
…4分(2)设

又

两式相加
 .
.所以
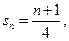 ………………6分
………………6分故
 ………………7分
………………7分又
 .故数列
.故数列 是等差数列.………………8分
是等差数列.………………8分(3)


要证:


即
 ………………10分
………………10分∵

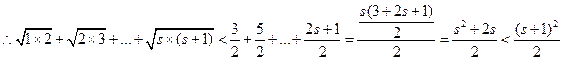 即
即 ,从而
,从而 ………………12分
………………12分又
 恒成立,
恒成立, 所以有
 恒成立
恒成立即


 …14分
…14分略

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 其中
其中 为预测期内年增长率,
为预测期内年增长率,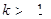 ,
, 为预测期人口数,
为预测期人口数, 为初期人口数,
为初期人口数,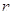 为预测期间隔年数。如果在某一时期有
为预测期间隔年数。如果在某一时期有 ,那么在这期间人口数
,那么在这期间人口数 的前
的前 项和为
项和为 ,
, ,
,
 ,求
,求 的值.
的值. 的前
的前 项和满足
项和满足 ,下列结论正确的是( )
,下列结论正确的是( ) 是
是 中最大值
中最大值

 的四个实根组成以
的四个实根组成以 为首项的等差数列,则
为首项的等差数列,则 
 C.
C. D.
D.
 }中,已知a1=
}中,已知a1= ,a2+a5=4,
,a2+a5=4, =242,求首项a1和项数n.
=242,求首项a1和项数n.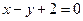 上。
上。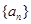 的前3项和
的前3项和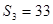 ,且
,且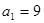 ,则
,则 ( )
( )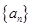 中,已知
中,已知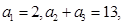 则
则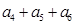 等于 ( )
等于 ( )