题目内容
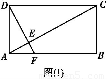
如图所示,矩形ABCD中,AB=a,AD=b,过点D作DE⊥AC于E,交直线AB于F.现将△ACD沿对角线AC折起到△PAC的位置,使二面角P AC
AC B的大小为60°.过P作PH⊥EF于H.
B的大小为60°.过P作PH⊥EF于H.
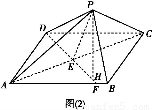
(1)求证:PH⊥平面ABC;
(2)若a+b=2,求四面体P ABC体积的最大值.
ABC体积的最大值.
【答案】
(1)见解析 (2) 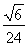
【解析】
(1)证明:∵DF⊥AC,
∴折起后AC⊥PE,AC⊥EF,
∴AC⊥平面PEF,
又PH?平面PEF,
∴AC⊥PH,
又PH⊥EF,EF∩AC=E,
∴PH⊥平面ABC.
(2)解:∵PE⊥AC,EF⊥AC,
∴∠PEF就是二面角P AC
AC B的平面角,
B的平面角,
∴∠PEF=60°,
∴Rt△PHE中,PH=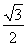 PE,
PE,
折起前,Rt△ADC中,
DE=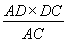 =
=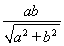 ,
,
S△ABC=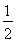 ab,
ab,
折起后,PE=DE,
∴PH=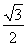 PE=
PE=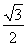 ·
·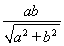 ,
,
∴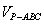 =
=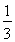 PH·S△ABC
PH·S△ABC
=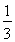 ·
·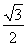 ·
·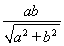 ·
·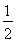 ab
ab
=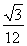 ·
· ,
,
∵a+b=2,a>0,b>0,
∴ ≤
≤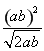 =
=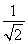
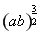 ≤
≤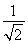
 =
=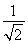 ,
,
当且仅当a=b=1时,两个等号同时成立,
因此(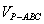 )max=
)max=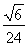 .
.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
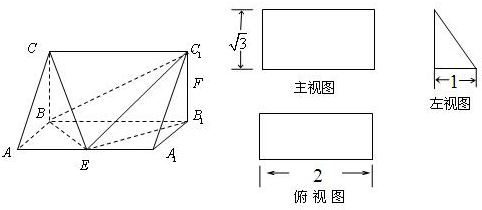
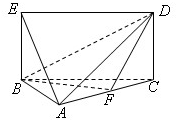 已知几何体A-BCDE如图所示,其中四边形BCDE为矩形,且BC=2,
已知几何体A-BCDE如图所示,其中四边形BCDE为矩形,且BC=2,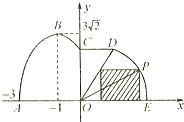 如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,
 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB=