题目内容
设a∈R,函数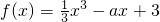 在区间(-2,-1)内是减函数,则实数a的取值范围________.
在区间(-2,-1)内是减函数,则实数a的取值范围________.
a≥4
分析:函数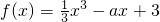 在区间(-2,-1)内是减函数,其导数在区间(-2,-1)内恒小于0,由此不等式解出实数a的取值范围
在区间(-2,-1)内是减函数,其导数在区间(-2,-1)内恒小于0,由此不等式解出实数a的取值范围
解答:∵函数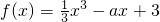
∴f′(x)=x2-a
又函数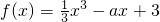 在区间(-2,-1)内是减函数
在区间(-2,-1)内是减函数
∴f′(x)=x2-a<0在区间(-2,-1)内成立
即a>x2区间(-2,-1)内恒成立
由于在区间(-2,-1)内x2∈(1,4)
所以a≥4
故答案为a≥4
点评:本题利用导数研究函数的单调性,解题的关键是理解并掌握函数的导数的符号与函数的单调性的关系,此类题一般有两类题型,一类是利用导数符号得出单调性,一类是由单调性得出导数的符号,本题属于第二种类型.
分析:函数
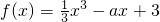 在区间(-2,-1)内是减函数,其导数在区间(-2,-1)内恒小于0,由此不等式解出实数a的取值范围
在区间(-2,-1)内是减函数,其导数在区间(-2,-1)内恒小于0,由此不等式解出实数a的取值范围解答:∵函数
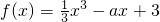
∴f′(x)=x2-a
又函数
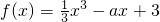 在区间(-2,-1)内是减函数
在区间(-2,-1)内是减函数∴f′(x)=x2-a<0在区间(-2,-1)内成立
即a>x2区间(-2,-1)内恒成立
由于在区间(-2,-1)内x2∈(1,4)
所以a≥4
故答案为a≥4
点评:本题利用导数研究函数的单调性,解题的关键是理解并掌握函数的导数的符号与函数的单调性的关系,此类题一般有两类题型,一类是利用导数符号得出单调性,一类是由单调性得出导数的符号,本题属于第二种类型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在区间(-2,-1)内是减函数,则实数a的取值范围 .
在区间(-2,-1)内是减函数,则实数a的取值范围 .