题目内容
已知等差数列{bn}的前n项和为Tn,且T4=4,b5=6.
(1)求数列{bn}的通项公式;
(2)若正整数n1,n2,…,nt,…满足5<n1<n2<…<nt,…且b3,b5,bn1,bn2,…,bnt,…成等比数列,求数列{nt}的通项公式(t是正整数);
(3)给出命题:在公比不等于1的等比数列{an}中,前n项和为Sn,若am,am+2,am+1成等差数列,则Sm,Sm+2,Sm+1也成等差数列.试判断此命题的真假,并证明你的结论.
(1)求数列{bn}的通项公式;
(2)若正整数n1,n2,…,nt,…满足5<n1<n2<…<nt,…且b3,b5,bn1,bn2,…,bnt,…成等比数列,求数列{nt}的通项公式(t是正整数);
(3)给出命题:在公比不等于1的等比数列{an}中,前n项和为Sn,若am,am+2,am+1成等差数列,则Sm,Sm+2,Sm+1也成等差数列.试判断此命题的真假,并证明你的结论.
分析:(1)本题是对数列的基本量的考查,根据通项公式、前n项和公式公式,算出公差和首项,写出通项公式.
(2)根据等比数列中前两项求出公比,写出通项bnt=b5•3t=2•3t+1 ,又bnt是{bn}中的第nt项,又可表示成bnt=2nt-4.根据这两式的相等性写出{nt}的通项.
(3)由am,am+2,am+1成等差数列,求出公比q=-
再利用等差数列定义判断Sm,Sm+2,Sm+1是否成等差数列.
(2)根据等比数列中前两项求出公比,写出通项bnt=b5•3t=2•3t+1 ,又bnt是{bn}中的第nt项,又可表示成bnt=2nt-4.根据这两式的相等性写出{nt}的通项.
(3)由am,am+2,am+1成等差数列,求出公比q=-
| 1 |
| 2 |
解答:解:(1)由已知,
,∴d=2,b1=-2,∴bn=b1+(n-1)d=2n-4.
(2)b3=2,且b3,b5,bn1,bn2,…,bnt,…成等比数列,所以公比q=
=3,所以bnt=b5•3t=2•3t+1,t∈N*.
又bnt=2nt-4,所以2nt-4=2•3t+1,所以nt=3t+1+2,t∈N*.
(3)此命题为真命题.
若am,am+2,am+1成等差数列,即a1q m-1+a1qm=2a1q m+1,移向化简整理得qm-1(2q2-q-1)=0,q=-
,
Sm+2-Sm=a m+1+a m+2=a m+2 (
+1)=-a m+2.Sm+1-Sm+2=-a m+2.∴Sm,Sm+2,Sm+1也成等差数列.
|
(2)b3=2,且b3,b5,bn1,bn2,…,bnt,…成等比数列,所以公比q=
| b5 |
| b3 |
又bnt=2nt-4,所以2nt-4=2•3t+1,所以nt=3t+1+2,t∈N*.
(3)此命题为真命题.
若am,am+2,am+1成等差数列,即a1q m-1+a1qm=2a1q m+1,移向化简整理得qm-1(2q2-q-1)=0,q=-
| 1 |
| 2 |
Sm+2-Sm=a m+1+a m+2=a m+2 (
| 1 |
| q |
点评:本题考查等差数列通项公式求解,等差数列的判定,等比数列的通项公式及应用.考查阅读分析、理解、计算能力.

练习册系列答案
相关题目
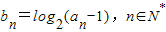 ,且已知a1=3,a3=9.
,且已知a1=3,a3=9. 为常数,则称数列{an}为“科比数列”.
为常数,则称数列{an}为“科比数列”.