题目内容
如图所示,在一个木制的棱长为3的正方体表面涂上颜色,将它的棱三等分,然后从每个等分点把正方体锯开,得到27棱长为1的小正方体,将这些小正方体充分混合后,装入一个口袋中.
(1)从这个口袋中任意取出1个小正方体,这个小正方体的表面恰好没有颜色的概率为多少?
(2)从这个口袋中同时任意取出2个小正方体,其中一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色的概率为多少?
解:在27个小正方体中,恰好有三个面都涂色有颜色的共有8个,恰好有两个都涂有颜色的共12个,恰好有一个面都涂有颜色的共6个,表面没涂颜色的1个.
(1)记“从这个口袋中任意取出1个小正方体,这个小正方体的表面恰好没有颜色”为事件A,则P(A)=![]() .
.
(2)从27个小正方体中同时任意取出2个小正方体,共![]() 种等可能的结果.这些结果中,有一个小正方体恰好有1面涂有颜色;另一个小正方体至少有2个面涂有颜色有
种等可能的结果.这些结果中,有一个小正方体恰好有1面涂有颜色;另一个小正方体至少有2个面涂有颜色有![]() 种.所以从27个小正方体中同时任意取出2个小正方体,有一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色概率为P=
种.所以从27个小正方体中同时任意取出2个小正方体,有一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色概率为P=![]() .
.

练习册系列答案
相关题目
 如图所示,在一个木制的棱长为3的正方体表面涂上颜色,将它的棱三等分,然后从每个等分点把正方体锯开,得到27个棱长为1的小正方体,将这些小正方体充分混合后,装入一个口袋中.从这个口袋中同时任意取出2个小正方体,其中一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色的概率为
如图所示,在一个木制的棱长为3的正方体表面涂上颜色,将它的棱三等分,然后从每个等分点把正方体锯开,得到27个棱长为1的小正方体,将这些小正方体充分混合后,装入一个口袋中.从这个口袋中同时任意取出2个小正方体,其中一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色的概率为
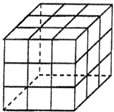 如图所示,在一个木制的棱长为3的正方体表面涂上颜色,将它的棱三等分,然后从每个等分点把正方体锯开,得到27个棱长为1的小正方体,将这些小正方体充分混合后,装入一个口袋中.从这个口袋中同时任意取出2个小正方体,其中一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色的概率为________.
如图所示,在一个木制的棱长为3的正方体表面涂上颜色,将它的棱三等分,然后从每个等分点把正方体锯开,得到27个棱长为1的小正方体,将这些小正方体充分混合后,装入一个口袋中.从这个口袋中同时任意取出2个小正方体,其中一个小正方体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色的概率为________.