题目内容
已知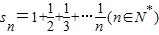 ,设f(n)=s2n+1-sn+1,试确定实数m的取值范围,使得对于一切大于1的正整数n,不等式
,设f(n)=s2n+1-sn+1,试确定实数m的取值范围,使得对于一切大于1的正整数n,不等式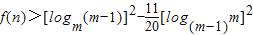 恒成立.
恒成立.
【答案】分析:根据定义,表示出f(n)=s2n+1-sn+1,从而函数f(n)为增函数,故可求函数的最小值.要使对于一切大于1的正整数n,不等式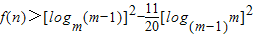 恒成立.所以只要
恒成立.所以只要 成立即可.利用换元法可求相应参数的范围.
成立即可.利用换元法可求相应参数的范围.
解答:解:由题意,f(n)=s2n+1-sn+1=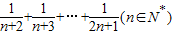
∵函数f(n)为增函数,∴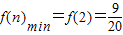
要使对于一切大于1的正整数n,不等式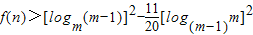 恒成立.
恒成立.
所以只要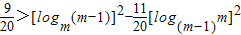 成立即可.
成立即可.
由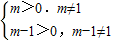 得m>1且m≠2
得m>1且m≠2
此时设[logm(m-1)]2=t,则t>0
于是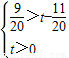 ,解得0<t<1
,解得0<t<1
由此得0<[logm(m-1)]2<1
解得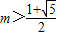 且m≠2
且m≠2
点评:本题的考点是函数恒成立问题.主要考查利用最值法解决恒成立问题,关键是利用函数的单调性求函数的最小值,考查不等式的求解,考查学生计算能力.
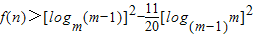 恒成立.所以只要
恒成立.所以只要 成立即可.利用换元法可求相应参数的范围.
成立即可.利用换元法可求相应参数的范围.解答:解:由题意,f(n)=s2n+1-sn+1=
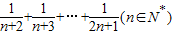
∵函数f(n)为增函数,∴
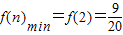
要使对于一切大于1的正整数n,不等式
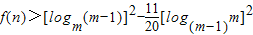 恒成立.
恒成立.所以只要
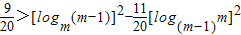 成立即可.
成立即可.由
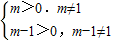 得m>1且m≠2
得m>1且m≠2此时设[logm(m-1)]2=t,则t>0
于是
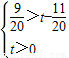 ,解得0<t<1
,解得0<t<1由此得0<[logm(m-1)]2<1
解得
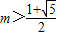 且m≠2
且m≠2点评:本题的考点是函数恒成立问题.主要考查利用最值法解决恒成立问题,关键是利用函数的单调性求函数的最小值,考查不等式的求解,考查学生计算能力.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目