题目内容
设数列{an}是等差数列,a1=1,Sn=a1+a2+…+an,数列{bn}是等比数列,Tn=b1+b2+…+bn,若a3=b2,S5=2T2-6,且![]() Tn=9.
Tn=9.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)当自然数n取何值时,Sn>Tn?
答案:
解析:
解析:
|
(Ⅰ)设 由 由前三式可得:45q(1-q)=18 而|q|<1,∴q= ∴代入条件得 (2) 令 ∵ 而 要使 由 可知n>4时, |

练习册系列答案
相关题目
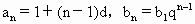 ,
,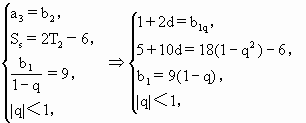
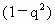 -6,解得:q=
-6,解得:q=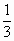 或q=
或q=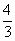 ,
,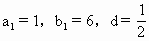
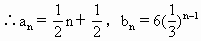
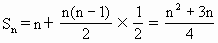
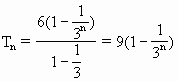
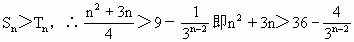
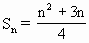 当n∈N时为增函数,
当n∈N时为增函数,
 ≥9
≥9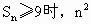 +3n≥36,检验n=4,5,…
+3n≥36,检验n=4,5,…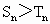 总成立,
总成立,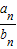 }的前n项和Sn.
}的前n项和Sn.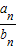 }的前n项和Sn.
}的前n项和Sn.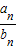 }的前n项和Sn.
}的前n项和Sn.