题目内容
下列几个结论:
①“x<-1”是“x<-2”的充分不必要条件;
②
(ex+sinx)dx=e-cos1;
③已知a>0,b>0,a+b=2,则y=
+
的最小值为
;
④若点(a,9)在函数y=3x的图象上,则tan
的值为-
;
⑤函数f(x)=2sin(2x-
)-1的对称中心为(
+
,0)(k∈Z).
其中正确的是
①“x<-1”是“x<-2”的充分不必要条件;
②
| ∫ | 1 0 |
③已知a>0,b>0,a+b=2,则y=
| 1 |
| a |
| 4 |
| b |
| 9 |
| 2 |
④若点(a,9)在函数y=3x的图象上,则tan
| aπ |
| 3 |
| 3 |
⑤函数f(x)=2sin(2x-
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
其中正确的是
②③④
②③④
(写出所有正确命题的序号)分析:由不等式的性质与充要条件的定义进行推理,得①不正确;由积分计算公式和微积分基本定理,可得②的积分计算正确;根据a+b=2将1=
(a+b)代入y表达式,再利用基本不等式算出y的最小值为
,得③正确;根据指数运算性质算出a=2,再由诱导公式和特殊角的三角函数值,算出tan
的值为-
,得④正确;根据三角函数图象的对称中心的公式,算出函数f(x)=2sin(2x-
)-1图象的对称中心为(
+
,1)(k∈Z),故⑤不正确.
| 1 |
| 2 |
| 9 |
| 2 |
| aπ |
| 3 |
| 3 |
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
解答:解:对于①,若“x<-1”成立,则“x<-2”不一定成立.
反之,若“x<-2”成立,则“x<-1”一定成立.
因此“x<-1”是“x<-2”的必要不充分条件,故①不正确;
对于②,由积分公式可得
(ex+sinx)dx=(ex-cosx)
=(e1-cos1)-(e0-cos0)=e-cos1,故②正确;
对于③,由于a>0,b>0,a+b=2,
可得y=
+
=
(a+b)(
+
)=
(5+
+
)≥
(5+2
)=
,
当且仅当b=2a=
时等号成立.
因此可得:y=
+
的最小值为
,故③正确;
对于④,若点(a,9)在函数y=3x的图象上,则9=3a,可得a=2.
∴tan
=tan
=-tan
=-
,故④正确;
对于⑤,对函数f(x)=2sin(2x-
)-1,令2x-
=kπ(k∈Z),可得x=
+
kπ(k∈Z),
所以函数f(x)=2sin(2x-
)-1图象的对称中心为(
+
,1)(k∈Z),故⑤不正确.
综上所述,正确的命题是②③④.
故答案为:②③④
反之,若“x<-2”成立,则“x<-1”一定成立.
因此“x<-1”是“x<-2”的必要不充分条件,故①不正确;
对于②,由积分公式可得
| ∫ | 1 0 |
| | | 1 0 |
对于③,由于a>0,b>0,a+b=2,
可得y=
| 1 |
| a |
| 4 |
| b |
| 1 |
| 2 |
| 1 |
| a |
| 4 |
| b |
| 1 |
| 2 |
| b |
| a |
| 4a |
| b |
| 1 |
| 2 |
|
| 9 |
| 2 |
当且仅当b=2a=
| 2 |
| 3 |
因此可得:y=
| 1 |
| a |
| 4 |
| b |
| 9 |
| 2 |
对于④,若点(a,9)在函数y=3x的图象上,则9=3a,可得a=2.
∴tan
| aπ |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 3 |
对于⑤,对函数f(x)=2sin(2x-
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
所以函数f(x)=2sin(2x-
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
综上所述,正确的命题是②③④.
故答案为:②③④
点评:本题给出几个命题,求出其中的真命题.着重考查了三角函数的图象与性质、三角函数的诱导公式、积分计算公式与微积分基本定理、利用基本不等式求最值和充要条件的判断等知识,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
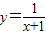 在(-∞,-1)∪(-1,+∞)上是减函数;
在(-∞,-1)∪(-1,+∞)上是减函数; ,则当x<0时,
,则当x<0时, ;
;