题目内容
给出下列命题：
①已知
⊥
，则
•(
+
)+
(
-
)=
•
；
②A、B、M、N为空间四点，若
，
，
不构成空间的一个基底，则A、B、M、N共面；
③已知
⊥
，则
，
与任何向量不构成空间的一个基底；
④已知{
，
，
}是空间的一个基底，则基向量
，
可以与向量
=
+
构成空间另一个基底．
正确命题个数是（ ）
①已知
| a |
| b |
| a |
| b |
| c |
| c• |
| b |
| a |
| b |
| c |
②A、B、M、N为空间四点，若
| BA |
| BM |
| BN |
③已知
| a |
| b |
| a |
| b |
④已知{
| a |
| b |
| c |
| a |
| b |
| m |
| a |
| c |
正确命题个数是（ ）
分析：对于①，由条件可得
•
=0，把等式的左边展开化简可得它和灯饰的右边相等，故①正确．
对于②，由条件可得
，
，
这3个向量共面，故A、B、M、N共面，故②正确．
对于③，若
与
，
这3个向量不共面，则 {
，
，
} 构成空间的一个基底，故③不正确．
对于④，由条件可得
=
+
与
，
这3个向量不共面，能构成空间的另一个基底，故④正确．
| a |
| b |
对于②，由条件可得
| BA |
| BM |
| BN |
对于③，若
| c |
| a |
| b |
| a |
| b |
| c |
对于④，由条件可得
| m |
| a |
| c |
| a |
| b |
解答：解：①若
⊥
，则
•
=0，故
•(
+
)+
(
-
)=
•
+
•
+
•
-
•
=0+
•
=
•
，
故①正确．
②若
，
，
不构成空间的一个基底，则
，
，
这3个向量共面，故A、B、M、N共面，
故②正确．
③当
⊥
时，若
与
，
这3个向量不共面，则 {
，
，
} 构成空间的一个基底，故③不正确．
④若{
，
，
}是空间的一个基底，设
=
+
，则
与
，
这3个向量不共面，
故{
，
，
} 构成空间的另一个基底，故④正确．
综上，①②④正确，③不正确．
故选：C．
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| c• |
| b |
| a |
| a |
| b |
| a |
| c |
| c |
| b |
| c |
| a |
| c |
| b |
| b |
| c |
故①正确．
②若
| BA |
| BM |
| BN |
| BA |
| BM |
| BN |
故②正确．
③当
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
④若{
| a |
| b |
| c |
| m |
| a |
| c |
| m |
| a |
| b |
故{
| a |
| b |
| m |
综上，①②④正确，③不正确．
故选：C．
点评：本题主要考查空间向量基本定理及其意义，三个向量能构成空间的基底的条件是，这三个向量不共面．
练习册系列答案
相关题目
”是“|2y-x|≤2”的充分不必要条件．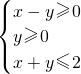
”是“|2y-x|≤2”的充分不必要条件．